More on Lindenmayer Systems

Sep 24, 2013

We briefly explored Lindenmayer systems (or L-systems) in an old post: Toying with Basic Fractals. We quickly reviewed this method for creation of an approximation to fractals, and displayed an example (the Koch snowflake) based on tikz libraries.

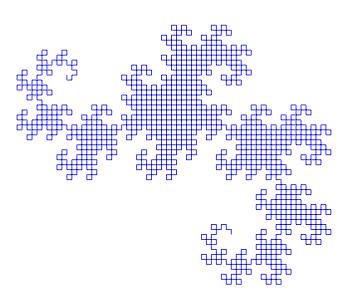
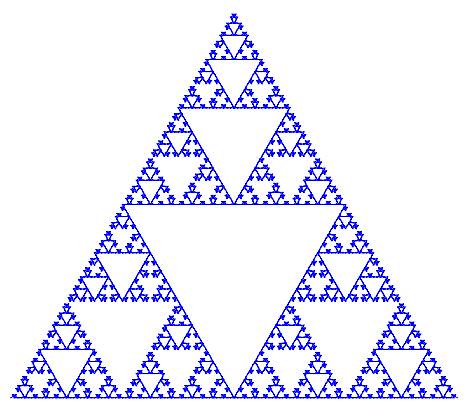
I would like to show a few more examples of beautiful curves generated with this technique, together with their generating axiom, rules and parameters. Feel free to click on each of the images below to download a larger version.

Note that any coding language with plotting capabilities should be able to tackle this project. I used once again tikz for \( \LaTeX \), but this time with the tikzlibrary lindenmayersystems.

name  : Dragon Curve
axiom : X
order : 11
step  : 5pt
angle : 90
rules :
        X -> X+YF+
        Y -> -FX-Y
 
name  : Gosper Space-filling Curve
axiom : XF
order : 5
step  : 2pt
angle : 60
rules :
	XF -> XF+YF++YF-XF--XFXF-YF+
	YF -> -XF+YFYF++YF+XF--XF-YF
 
name  : Quadric Koch Island
axiom : F+F+F+F
order : 4
step  : 1pt
angle : 90
rules :
        F -> F+F-F-FF+F+F-F
        .
 
name  : Sierpinski Arrowhead
axiom : F
order : 8
step  : 3.5pt
angle : 60
rules :
        G -> F+G+F
        F -> G-F-G
 
name  : ?
axiom : F+F+F+F
order : 4
step  : 2pt
angle : 90
rules :
        F -> FF+F+F+F+F+F-F
 
name  : ?
axiom : F+F+F+F
order : 4
step  : 3pt
angle : 90
rules :
        F -> FF+F+F+F+FF

Would you like to experiment a little with axioms, rules and parameters, and obtain some new pleasant curves with this method? If the mathematical properties of the fractal that they approximate are interesting enough, I bet you could attach your name to them. Like the astronomer that finds through her telescope a new object in the sky, or the zoologist that discover a new species of spider in the forest.