MATH 300 Fall 2018 Problems from Chapter 11
Relations
The following is the list of problems for sections 11.0 and 11.1 of the Book of Proof (pages 178 and 182).
There is a forum open at the end, so you can ask questions. It is a great way to interact with the instructor and with
other students in your class, should you need some assistance with any question. Please, do not post
solutions.
Exercises for Section 11.0
- Let \( A = \{ 0, 1, 2, 3, 4, 5\}. \) Write out the relation \( R \) that expresses \( > \) on \( A. \) Then illustrate it with a diagram.
- Let \( A = \{ 1, 2, 3, 4, 5, 6 \}. \) Write out the relation \( R \) that expresses \( \vert \) (divides) on \( A. \) Then illustrate it with a diagram.
- Let \( A = \{ 0, 1, 2, 3, 4, 5 \}. \) Write out the relation \( R \) that expresses \( \geq \) on \( A. \) Then illustrate it with a diagram.
- Here is a diagram for a relation \( R \) on a set \( A. \) Write the sets \( A \) and \( R. \)
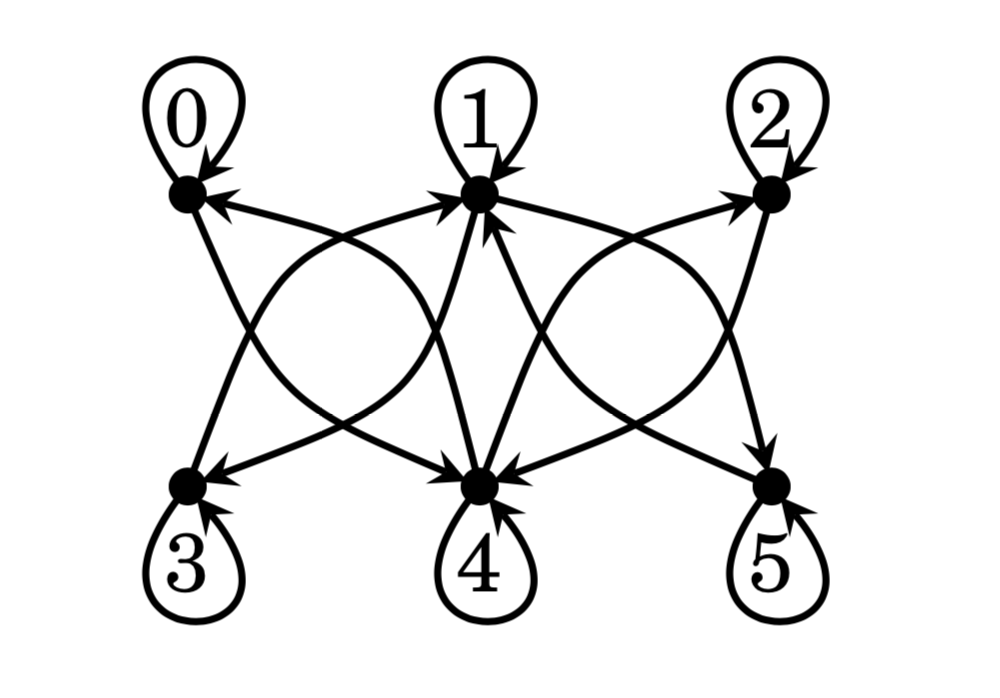
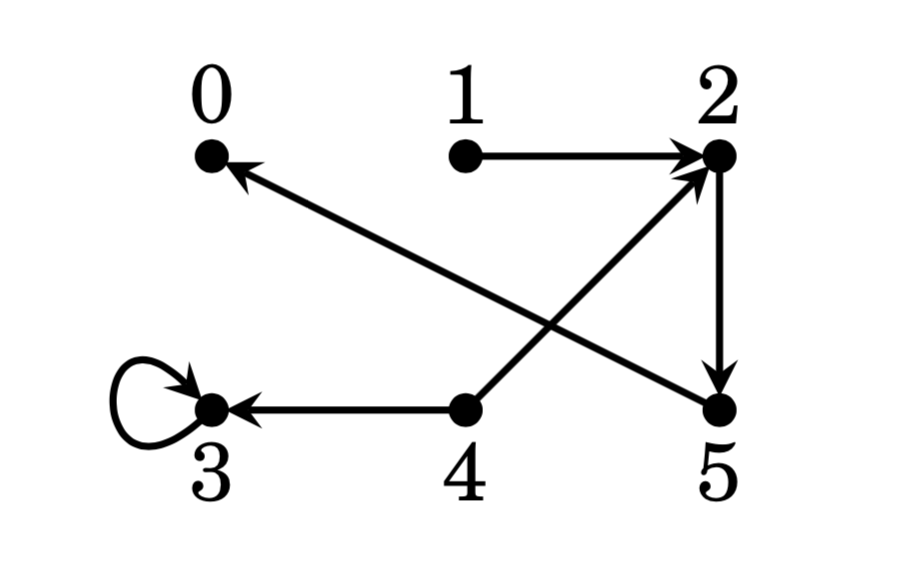
- Here is a diagram for a relation \( R \) on a set \( A. \) Write the sets \( A \) and \( R. \)
- Congruence modulo 5 is a relation on the set \( A = \mathbb{Z}. \) In this relation \( xRy \) means \( x \equiv y \pmod{5}. \) Write out the set \( R \) in set-builder notation.
- Write the relation \( < \) on the set \( A = \mathbb{Z} \) as a subset \( R \) of \( \mathbb{Z} \times \mathbb{Z}. \) This is an infinite set, so you will have to use set-builder notation.
- Let \( A = \{ 1, 2, 3, 4, 5, 6\}. \) Observe that \( \emptyset \subseteq A \times A, \) so \( R = \emptyset \) is a relation on \( A. \) Draw a diagram of this relation.
- Let \( A = \{ 1, 2, 3, 4, 5, 6\}. \) How many different relations are there on the set \( A \)?
- Consider the subset \( R = ( \mathbb{R} \times \mathbb{R} ) \setminus \{ (x,x) : x \in \mathbb{R} \} \subseteq \mathbb{R} \times \mathbb{R}. \) What familiar relation on \( \mathbb{R} \) is this?
- Given a finite set \( A, \) how many different relations are there on \( A \)?
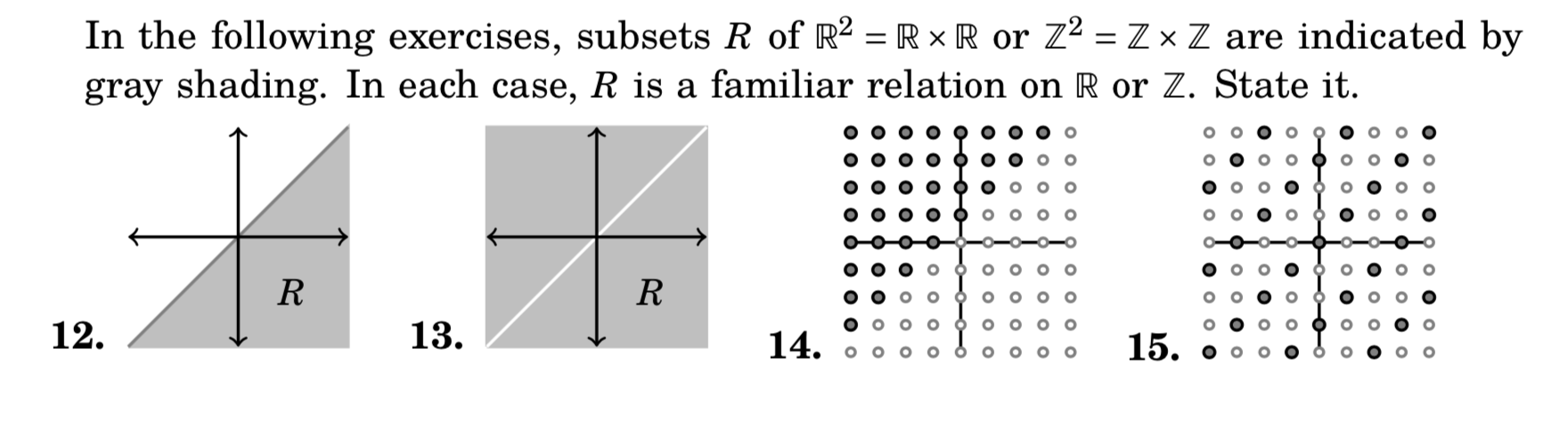
Exercises for Section 11.1
- Consider the relation \( R = \{ (a,a), (b,b), (c,c), (d,d), (a,b), (b,a) \} \) on set \( A = \{ a, b, c, d \}. \) Is \( R \) reflexive? Symmetric? Transitive? If a property does not hold, say why.
- Consider the relation \( R = \{ (a,b), (a,c), (c,c), (b,b), (c,b), (b,c) \} \) on set \( A = \{ a, b, c \}. \) Is \( R \) reflexive? Symmetric? Transitive? If a property does not hold, say why.
- Consider the relation \( R = \{ (a,b), (a,c), (c,b), (b,c) \} \) on set \( A = \{ a, b, c \}. \) Is \( R \) reflexive? Symmetric? Transitive? If a property does not hold, say why.
-
Let \( A = \{ a, b, c, d \}. \) Suppose \( R \) is the relation \( \begin{align} R = \{ &(a,a), (b,b), (c,c), (d,d), (a,b), (b,a), (a,c), (c,a), \cr &(a,d), (d,a), (b,c), (c,b), (d,b), (d,b), (c,d), (d,c) \}. \end{align} \)
Is \( R \) reflexive? Symmetric? Transitive? If a property does not hold, say why.
- Consider the relation \( R = \{ (0,0), (\sqrt{2},0), (0,\sqrt{2}), (\sqrt{2}, \sqrt{2}) \} \) on \( \mathbb{R}. \) Is \( R \) reflexive? Symmetric? Transitive? If a property does not hold, say why.
- Consider the relation \( R = \{ (x,x) : x \in \mathbb{Z} \} \) on \( \mathbb{Z}. \) Is \( R \) reflexive? Symmetric? Transitive? If a property does not hold, say why. What familiar relation is this?
- There are 16 possible different relations on the set \( A = \{ a, b \}. \) Describe all of them. (A picture of each will suffice, but don’t forget to label the nodes.) Which ones are reflexive? Symmetric? Transitive?
- Define a relation on \( \mathbb{Z} \) as \( x\operatorname{R}y \) if \( \lvert x-y \rvert < 1. \)
Is \( R \) reflexive? Symmetric? Transitive? If a property does not hold, say why. What familiar relation is this? - Define a relation on \( \mathbb{Z} \) by declaring \( x \operatorname{R} y \) if and only if \( x \) and \( y \) have the same parity. Is \( R \) reflexive? Symmetric? Transitive? If a property does not hold, say why. What familiar relation is this?
- Suppose \( A \neq \emptyset. \) Since \( \emptyset \subseteq A \times A, \) the set \( R = \emptyset \) is a relation on \( A. \) Is \( R \) reflexive? Symmetric? Transitive? If a property does not hold, say why.
- Suppose \( A = \{ a, b, c, d \} \) and \( R = \{ (a,a), (b,b), (c,c), (d,d) \}. \) Is \( R \) reflexive? Symmetric? Transitive? If a property does not hold, say why.
- Prove that the relation \( \vert \) (divides) on the set \( \mathbb{Z} \) is reflexive and transitive. (Use example 11.8 as a guide if you are unsure on how to proceed.)
- Consider the relation \( R = \{ (x,y) \in \mathbb{R} \times \mathbb{R} : x - y \in \mathbb{Z} \} \) on \( \mathbb{R}. \) Prove that this relation is reflexive, transitive and symmetric.
- Suppose \( R \) is a symmetric and transitive relation on a set \( A, \) and there is an element \( a \in A \) for which \( a \operatorname{R} x \) for every \( x \in A. \) Prove that \( R \) is reflexive.
- Prove or disprove: If a relation is symmetric and transitive, then it is also reflexive.
- Define a relation \( R \) on \( \mathbb{Z} \) by declaring that \( x \operatorname{R} y \) if and only if \( x^2 \equiv y^2 \pmod{4}. \) Prove that \( R \) is reflexive, symmetric and transitive.
- Modifying the above exercise 8 slightly, define a relation \( R \) on \( \mathbb{Z} \) as \( x \operatorname{R} y \) if and only if \( \lvert x-y \rvert \leq 1. \) Say whether \( R \) is reflexive. Is it symmetric? Transitive?
- The table on page 179 shows that relations on \( \mathbb{Z} \) may obey various combinations of the reflexive, symmetric and transitive properties. In all, there are \( 2^3 = 8 \) possible combinations, and the table shows 5 of them. (There is some redundancy, as \( \leq \) and \( \vert \) have the same type.) Complete the table by finding examples of relations on \( \mathbb{Z} \) for the three missing combinations.