The Cantor Pairing Function

The objective of this post is to construct a pairing function, that presents us with a bijection between the set of natural numbers, and the lattice of points in the plane with non-negative integer coordinates.

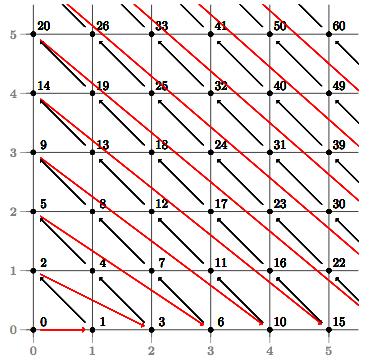
We will accomplish this by creating the corresponding map (and its inverse), that takes each natural number \( z \) and drops it at a location in the lattice, as the following diagram suggests:

That is: the zero goes at the origin, and then we populate the two positions in the diagonal \( x+y=1 \). Then we populate the three positions in the diagonal \( x+y=2 \), and so on. Note that by doing so, when we are done populating the last \( n+1 \) positions of the \( n \)–th diagonal, we have placed \( 1+2+3+\dotsb+(n+1) = \tfrac{(n+1)(n+2)}{2} \) natural numbers (including the zero!) in the lattice.

In particular, note that the triangular numbers \( t_n = 1 + 2 + \dotsb + n \) occupy all the positions in the \( x \)–axis, precisely where this one intersects the lines \( x+y=n\).

This is the key ingredient to construct the required bijection: Given a natural number \( z \in \mathbb{N}, \) there is a unique value \( n = n(z) \) such that \( t_n \leq z < t_{n+1} \) (since the sequence of triangular numbers is strictly increasing). The number \( z \) then belongs to the intersection of the lattice with the diagonal line \( x+y=n, \) and it only remains to know how far from the \( x \)–axis: the offset \( z-t_n \) actually indicates the \( y \) coordinate of the position of \( z \) in the lattice. We can now find the precise position of \( z \) by solving the following simple system of two equations with two variables:

Or simply put, the coordinates are given by \( x=n(z)-z+t_{n(z)} \), \( y=z-t_{n(z)}. \) The question remaining is, of course, how to find the value of \( n(z). \)

We need to look for the value of \( n \) such that

One way to accomplish this is to find the closest natural number \( n \) to the solution of either side of the inequalities above, say \( n^2 + n -2z = 0. \) By choosing this side, an appropriate expression for this value is given by

We have successfully computed for each natural number \( z \in \mathbb{N} \cup { 0 } \) a unique position in the lattice \( \big( \mathbb{N} \cup { 0 }\big)^2. \) The construction is also such that for each position \( (x,y) \) in the previous lattice, there is a unique natural number that can be sent to that position. The corresponding expression will lead us to the construction of the inverse function \( \pi^{-1} \colon \big( \mathbb{N} \cup { 0 } \big)^2 \to \mathbb{N} \cup { 0 }. \) The key is again the same system of equations as before:

Given \( (x,y), \) we find \( n=x+y. \) This leads us to compute the corresponding \( t_n, \) and the second equations gives us

Miscellaneous

Antoine Flattot suggests using this construction to find a proof that the natural numbers are also in bijection with the rational numbers, and thus they both have the same cardinality. How would the reader go about it?

Also, by using either function above we can obtain elegant diagrams in \( \LaTeX \) with the tikz package, showing graphically the structure of the location assignments. For example, with the choice of \( \pi, \) we could write a simple function to assign all \( z+1 \) positions from 0 to \( z, \) including arrows pointing the direction in which the sequence progresses:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
\def\gCpf#1{
% Compute the maximum width of the box that contains all values
% from 0 to #1
\pgfmathparse{0.5+floor(0.5*(sqrt(8*#1+1)-1))}
\let\width\pgfmathresult
% Generate a grid with the corresponding width
\draw (-0.25cm,-0.25cm) grid[step=2cm,ultra thin,gray]
	(2*\width cm+0.25cm, 2*\width cm+0.25cm);
\foreach \x in {0,...,\width} {
	\draw[gray,ultra thin] (2*\x,0.2cm-0.25cm) --
		(2*\x, -0.2cm-0.25cm) node[below]
		{\large $\boldsymbol{\x} $};
	\draw[gray,ultra thin] (0.2cm-0.25cm,2*\x) --
		(-0.2cm-0.25cm,2*\x) node[left]
		{\large $\boldsymbol{\x} $};
% First node, always at the origin
\filldraw(0,0) circle (2pt);
\draw(10pt,8pt) node{\large $0 $};

% For each number z between 1 and #1...
\foreach \n in {1,..., #1}
{
	% Compute the diagonal number n(z) and the previous
	\pgfmathparse{floor(0.5*(sqrt(8*\n+1)-1))}
	\let\thisn\pgfmathresult
	\pgfmathparse{floor(0.5*(sqrt(8*\n-7)-1))}
	\let\prevn\pgfmathresult
	%Compute the triangular number t_n and the previous
	\pgfmathparse{0.5*(\thisn^2+\thisn)}
	\let\thist\pgfmathresult
	\pgfmathparse{0.5*(\prevn^2+\prevn)}
	\let\prevt\pgfmathresult
	% Compute the y coords of this and the previous
	\pgfmathparse{\n-\thist}
	\let\thisy\pgfmathresult
	\pgfmathparse{\n-1-\prevt}
	\let\prevy\pgfmathresult
	% Compute the x coords of this and the previous
	\pgfmathparse{\thisn-\thisy}
	\let\thisx\pgfmathresult
	\pgfmathparse{\prevn-\prevy}
	\let\prevx\pgfmathresult
	% Done.  Let's place the nodes at their locations
	\node (this) at (2*\thisx,2*\thisy) [inner sep=6pt] {};
	\node (prev) at (2*\prevx,2*\prevy) [inner sep=6pt] {};
	\draw (2*\thisx cm+10pt,2*\thisy cm+8pt) node{\large $\n $};
	\filldraw (2*\thisx cm,2*\thisy cm) circle (2pt);
	% If the node belongs in the x-axis, receive a red arrow
	% Otherwise, a black arrow
	\ifthenelse{\lengthtest{\thisy cm = 0 cm}}{
		\draw[->,thick,red] (prev) -- (this);
	}{
		\draw[->] (prev) -- (this);
	}
}

Note that the \( \LaTeX \) libraries calc and ifthen need to be loaded previously, to be able to handle some of the commands.