This document summarizes my progression as an instructor, teaching philosophy and goals. It contains four parts: in the first one, I enumerate the different assignments in which I have participated at the University level, with a brief description of my duties. Where available and relevant, I also include short statistics of the results of my teaching evaluations. I summarize my views on instruction and education on a second paragraph. On a third section, I include a description of some of the courses and topics for which I am passionate, and for which I can make a strong contribution as an educator. I ended with practical examples of my previous statements, including one of my latest syllabi, teaching evaluations, lesson plans and slides for some of my more advanced classes, and interaction with students through my professional blog. I believe they strongly support my pursue of excellence in teaching.

Teaching Assignments

  • Grader and recitation instructor for all 100 and 200 levels of Algebra/Trigonometry (pre-Calculus), Calculus (including Business and honor Calculus), 300 level Geometry, and Differential Equations at Purdue University. Average recitation evaluation near 5/5.
  • Main lecturer for almost all 100 and 200 levels of Mathematics at Purdue University, including all courses in the Algebra/Trigonometry series (pre-Calculus), and all Calculus courses. Average instructor evaluation over 4/5.
  • Main lecturer for all 100 and 200 levels of Calculus (including Business Calculus and Elementary Differential Equations) at the University of South Carolina. Average instructor evaluation over 4/5.
  • Main lecturer for 300 level courses in Geometry and Differential Equations at Purdue University. Average instructor evaluation over 4/5.
  • Recitation instructor for graduate-level courses on Abstract Algebra and Partial Differential Equations at the University of Minnesota. No instructor evaluation offered.
  • Main lecturer for a graduate-level summer course on Measure Theory at Purdue University. No instructor evaluation offered.
  • Main lecturer for a reading course on Mathematical Imaging at the University of South Carolina. No instructor evaluation offered.
  • Programmer for the SAGE project (Student Assignments Graded Electronically) at Purdue University, helping develop a computer-based homework system. This appointment required not only strong coding abilities, but also a deep familiarity with all courses offered in the department of Mathematics, and in particular all minute details of each homework assignment. It also required working closely with instructors, course coordinators, and students simultaneously.

Teaching Philosophy

I base my teaching philosophy on two concepts: feedback and motivation. My approach to lectures is classical, in the sense that I feel more comfortable interacting with my students in front of either a blackboard, or an interactive screen, going over theory and posterior problem solving. The structure of each class allows me to obtain as much feedback from my students as possible, and this accomplishes two important goals:

  • The speed and order in which new material is covered depends mostly on the background of the students, and not solely based on a rigorous syllabus.
  • In case of a student’s failure in the course, I have enough information to provide very accurate and personalized advise.

Motivation plays a big role in my teaching principles. I use it, for example, to raise awareness of unsolved questions, or current applications to real-life situations that are close to their interests. I can push this a little further and, with the right guidance, offer all my students the opportunity to research at their level on a topic for which they are passionate.

In the stage where motivation comes into play, I deviate from traditional methods in favor of new technologies. For example, my students benefit from the interaction with my professional blog, where they can obtain course-related material and network with their classmates. I have attached an example to this document. I am extremely proficient on the use of Mathematical engines (Maple, MATLAB, Mathematica, sage, etc.) and scientific typesetting with \( \LaTeX \). I use these skills to create visual examples, or generate enough different problems with certain characteristics. I have also included another example to support this claim, from one 400-level Geometry class I taught at Purdue University.

A good example of the benefits of this methodology can be readily observed on some of my students’ research projects every semester: study of the behavior of the oil slick in the Gulf of Mexico, applications to financial mathematics, dynamics of networks of enzymes, improvement of metal structures subject to vibrations, study of tension on strings, artificial intelligence, etc. Some of these projects have even received coverage in the news. I have included some of these projects in their corresponding course-pages online for future reference, and I encourage the readers to take a minute to examine them.

In summary: My recipe for success in education starts by supporting students’ passion through motivation. It is accomplished by helping them achieve their goals by putting emphasis on their stronger skills. It is improved by identifying shortcomings in their scientific background and helping them overcome those issues.

Future Goals

Among all the possible undergraduate-level courses available, I am especially interested in those where several different mathematical techniques come together: differential equations, linear algebra, discrete mathematics, pattern recognition or data mining, to name a few. It is not only the beauty of the material that drives my interest, but the countless possibilities to guide students in the application of these topics to interesting research projects.

I am also capable of teaching both at the advanced-undergraduate and graduate levels. In the past ten years I have been working on my particular take of some topics for which I am extremely passionate: In the theoretical arena, the fields of algebraic topology, theory of distributions and differential geometry; in the field of practical mathematics, applications of functional analysis, the theory of distributions, variational methods, partial differential equations, approximation theory and numerical methods to mathematical imaging. I have been typing extensive notes and posting online examples of lectures and assignments, again through my professional blog. Once more I point the reader to that resource for a more detailed review of my potential as instructor.

Example of Use of Technology in the Classroom

An IGSE (Interactive Geometry Software Environment) is a computer program that helps create dynamic diagrams in different Geometries (planar or 3D Euclidean, or even spherical or hyperbolic). It allows the user to drop points on screen, or select two points to construct the segment through them, or the circle centered in the first that goes through the second, etc. Once done with a geometric construction, it is possible to click and hold on any of its elements (let it be a point, a segment, a circle, etc.) and while dragging them all over the screen, change the shape of the construction. It is a very valuable tool that allows students to gain a huge insight and intuition on geometric structures, and has helped many a mathematician to pose and solve interesting problems. The best exponent of these IGSEs is probably GeoGebra, with which I am very proficient, and have used it in countless occasions to carry my lectures or Summer Research Projects.

The usual way to include diagrams from an IGSE in a document is by asking the software to produce a proper image, or by grabbing screen shots. But with tikz and a few of its libraries, one can mass produce these diagrams within \( \LaTeX \) code, without the need of a IGSE. The figure below was generated as a tabular with four centered columns, and on each cell of the table a function holding a tikzpicture environment was included. The function produces a random example of the Theorem below.

Consider three circles \( c_1, c_2, c_3\) that intersect in a common point \(O\). (see figure above) Circles \(c_1\) and \(c_2\) intersect also at point \(A\). Circles \(c_2\) and \(c_3\) intersect also at point \(B\). Circles \(c_1\) and \(c_3\) intersect also at a point \(C\). Consider any point \(P \in c_1\), and trace a line through \(P\) and \(A\). This line intersects circle \(c_2\) at a second point \(P'\). Trace a line through \(P'\) and \(B\). This line intersects circle \(c_3\) at a second point \(P''\). We want to prove that the points \(P,P''\) and \(C\) are collinear.

Example of Lesson Plans and Handouts

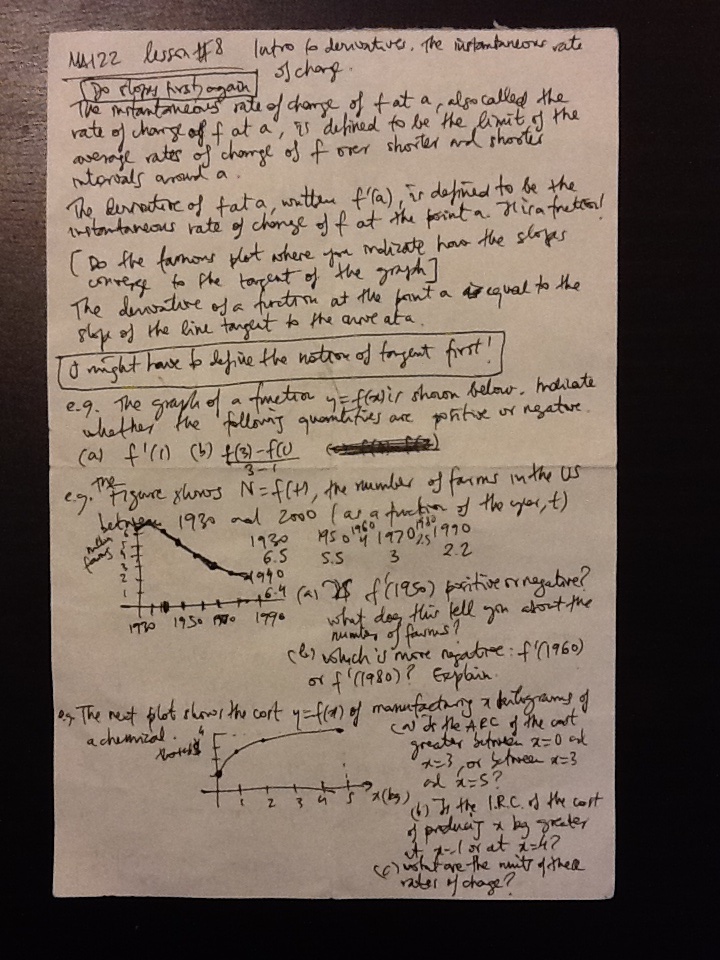
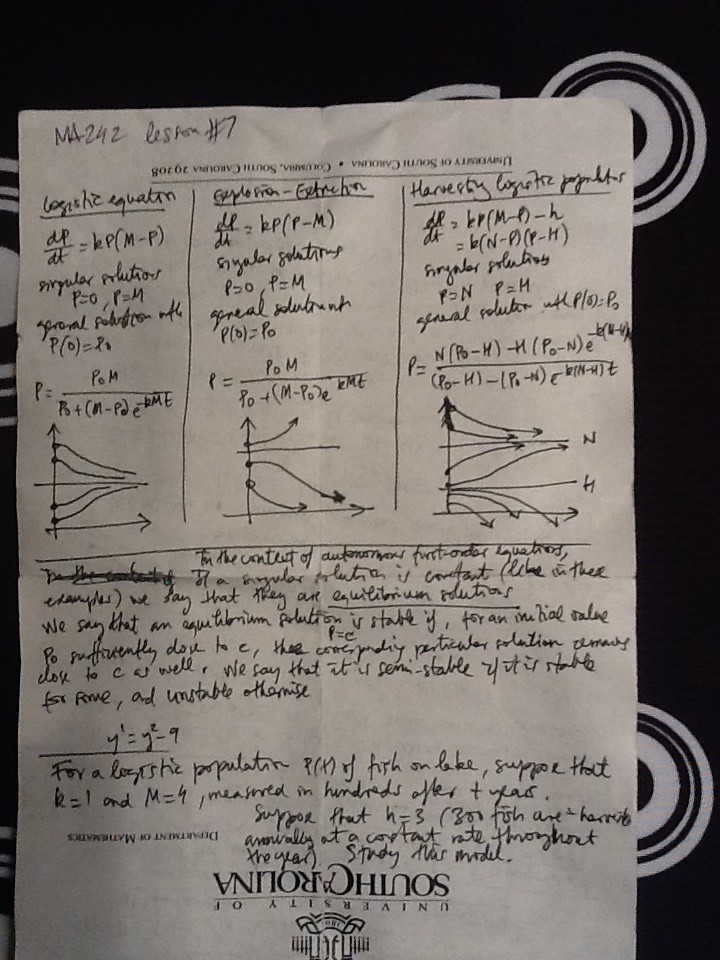
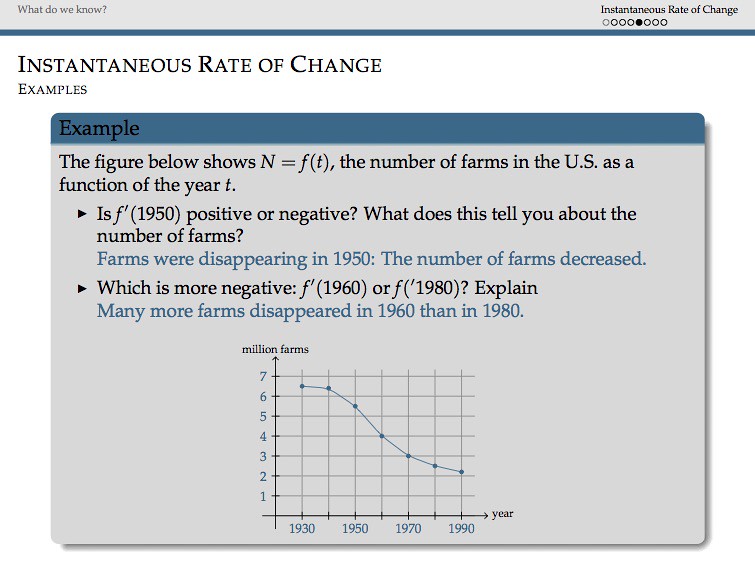
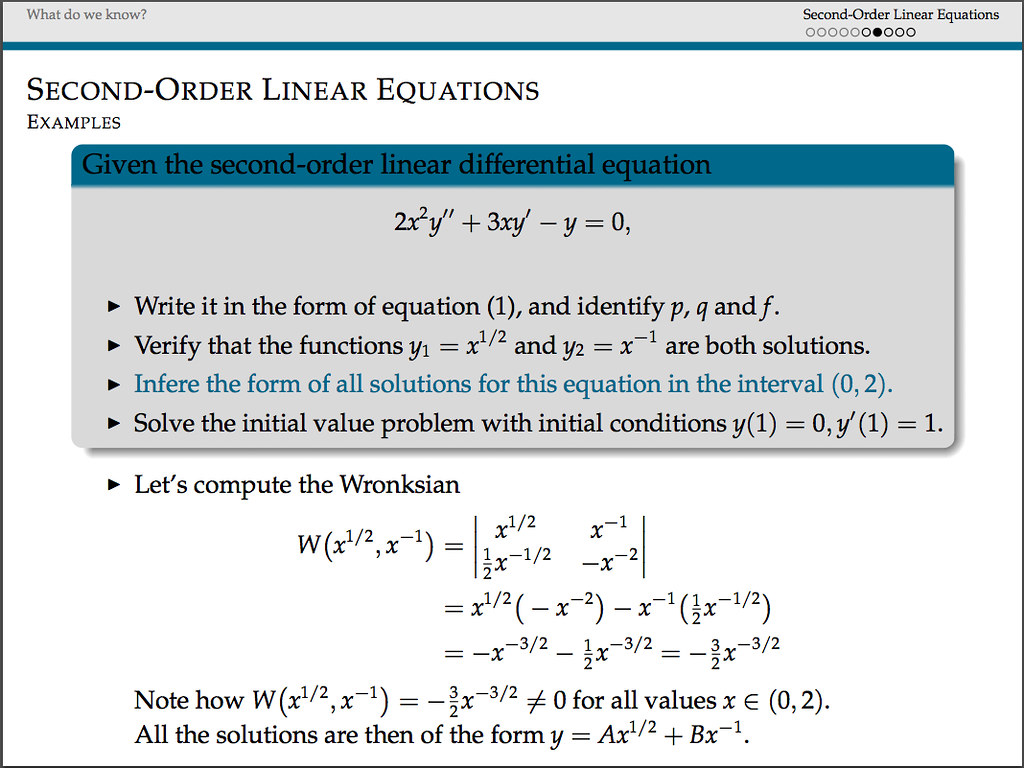
I keep all lesson plans in Evernote and Dropbox for future reference, as well as resources for my students. The following are examples from some of the most relevant lessons of some of my classes at UofSC.


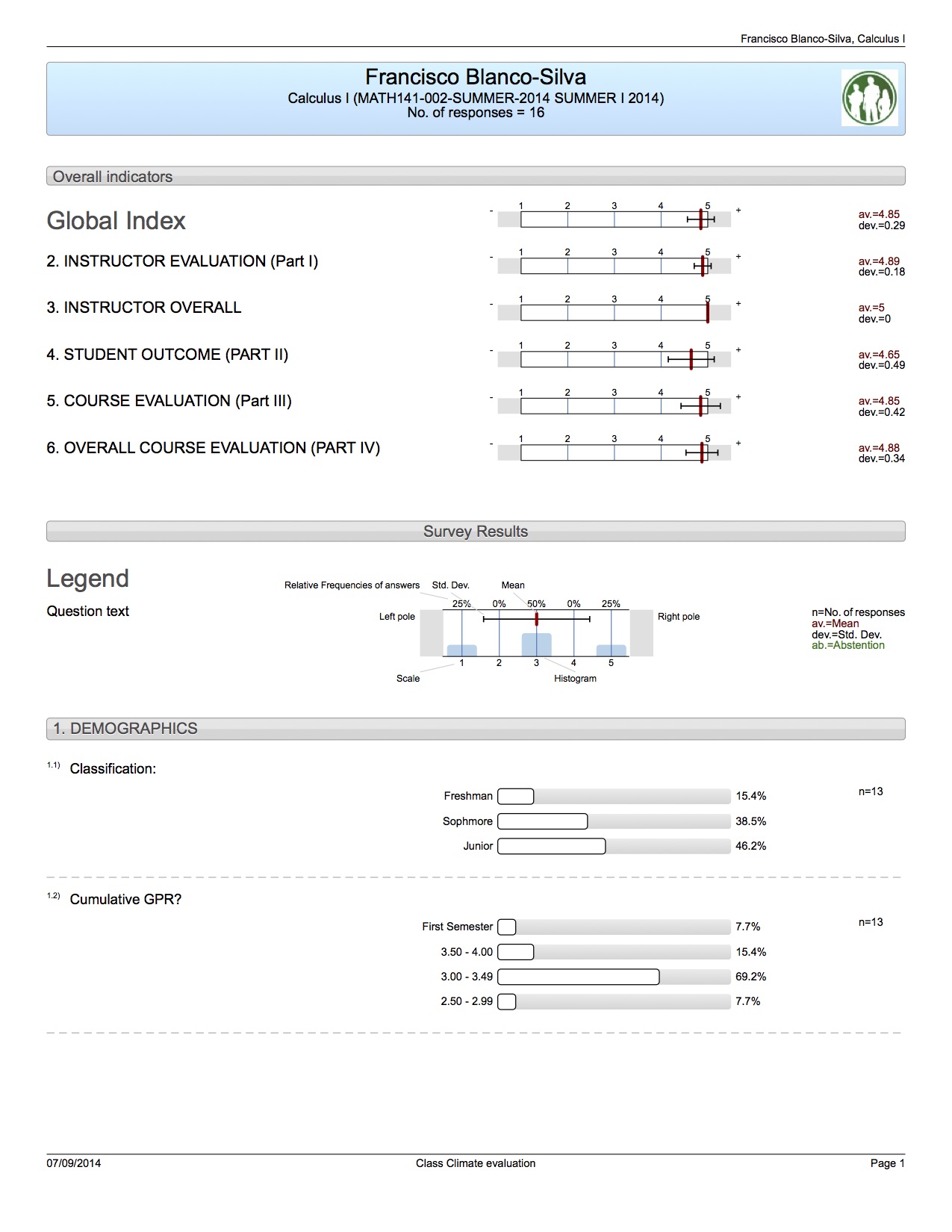
Example of Teaching Evaluations

The following is the first page of one of the most recent “climate class surveys” administered in one of my lectures of Calculus I. It indicates the students’ appraisal of my general performance, as well as a course evaluation.

Example of Recent Syllabus

You can see all my syllabi online through the Teaching tab on this blog.

Example of Student Interaction on a Practice Exam Online

For selected in-class exams, I often prepare a practice exam online. I do not include an answer key on these online; instead I create a forum for the students — the intention is precisely to foster interaction among them, besides the obvious preparation of the material. Examples of this interaction can be retrieved through the Teaching tab on this blog.