Apollonian gaskets and circle inversion fractals

Recall the definition of an iterated function system (IFS), and how on occasion, their attractors are fractal sets. What happens when we allow more general functions instead of mere affine maps?

The key to the design of this amazing fractal is in the notion of limit sets of circle inversions.

The definition of inversion \( f_C \colon \mathbb{C} \to \mathbb{C} \) with respect to a circle \( C \) with center \( \boldsymbol{c} \in \mathbb{C} \) and radius \( r>0 \) depends on the location of \( z\in \mathbb{C} \) with respect to the circle:

• Given any point \( z\in \mathbb{C} \) outside of the disk bounded by \( C, \) consider the segment that joins \( \boldsymbol{c} \) with \( z, \) and the only circle that has this segment as diameter. The two circles intersect at points \( P, Q. \) The intersection of the segments \( PQ \) and \( \boldsymbol{c}z \) is the inversion of \( z\colon \)

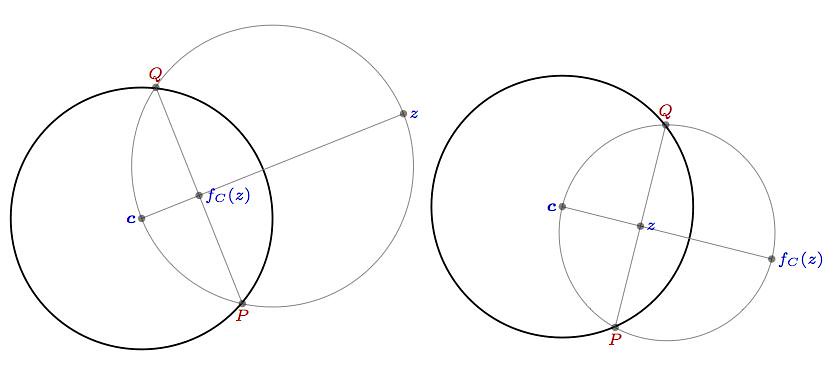
• The inversion of a point \( z \) inside the disk bounded by \( C \) is obtained in a similar fashion: Consider the ray originating at \( \boldsymbol{c} \) that goes through \( z, \) and its perpendicular through \( z. \) The latter intersects the circle \( C \) at points \( P,Q. \) The only circle that goes through \( \boldsymbol{c}, P \) and \( Q \) intersects the ray \( \boldsymbol{c}z \) at the inversion of \( z. \)
• For any point \( z \) in the circle \( C, \) it is \( f_C(z)=z. \)

Note that the circle inversion is an involution: \( \big( f_C\circ f_C\big) (z) = z \) for all \( z \in \mathbb{C}. \) One must therefore be careful when designing IFS’s with inversions; usually we include a mechanism that prevents such a map to be called twice on a row.

Let us examine a few basic examples:

An IFS consisting on circle inversions with respect to two disjoint disks

Choose two disjoint disks, construct an IFS containing the two corresponding circle inversions, pick a random point outside the two disks, and compute the orbit of this point by mapping each output through alternate inversions (in order to avoid the involution producing infinite loops). As you can see in the figure below, the limit seems to be a very simple set: two points. Can you find their location analytically?

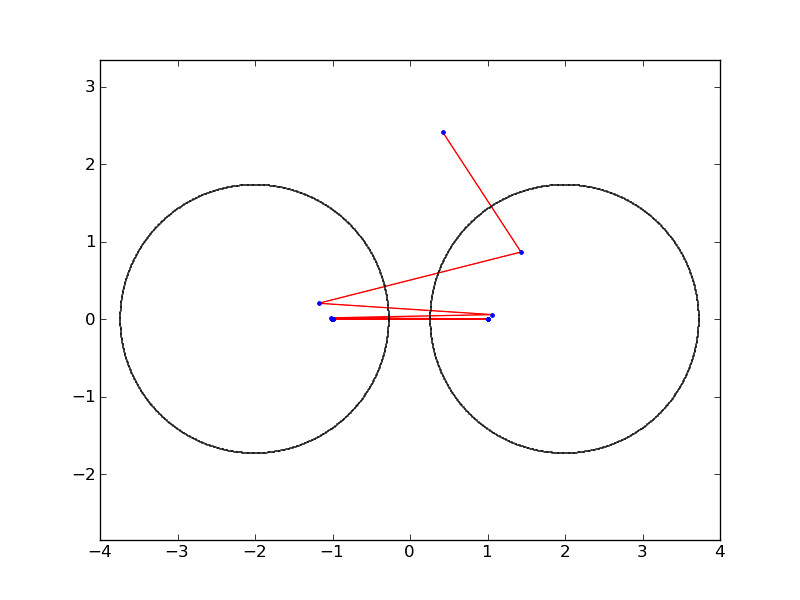
How will the attractor set change if the two disks are tangent? And if the two disks intersect at a larger set?

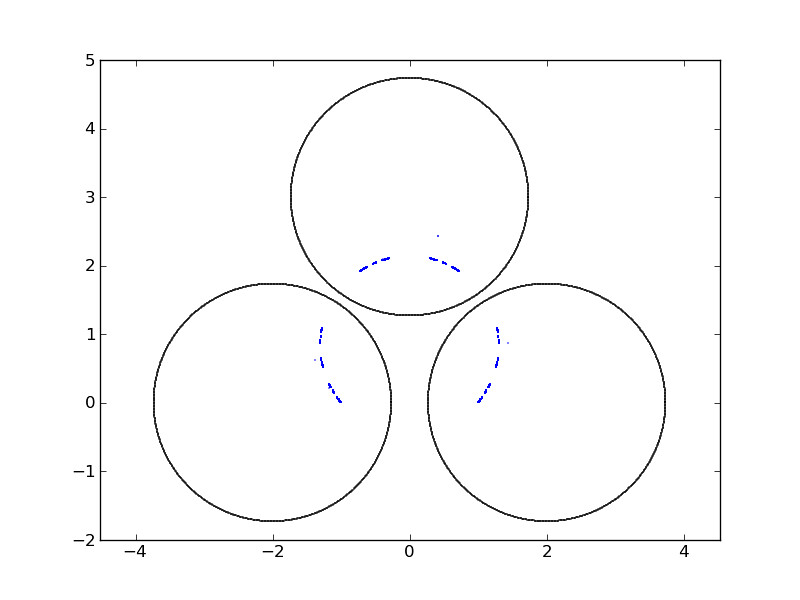
An IFS consisting on circle inversions with respect to three mutually disjoint disks

We obtain our first fractal: It has the structure of a Cantor set, supported on a circle. Can you find the center and radius of that circle?

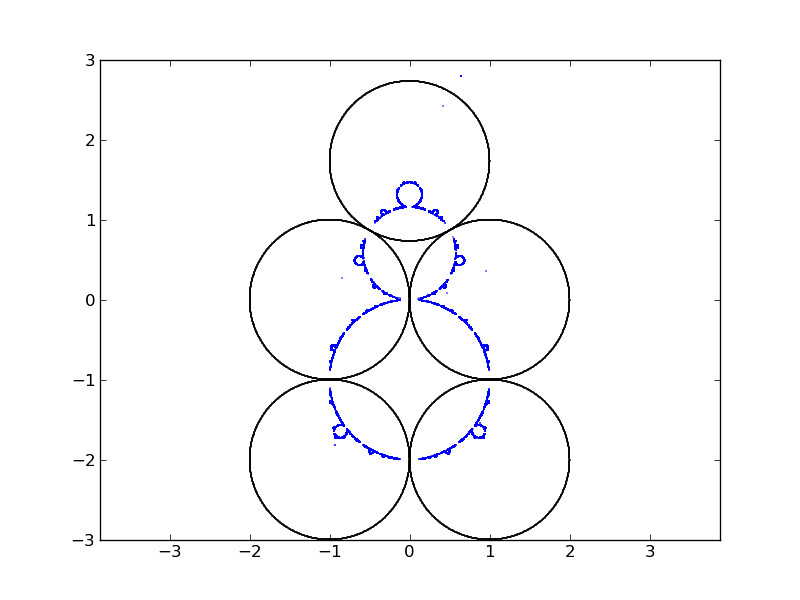
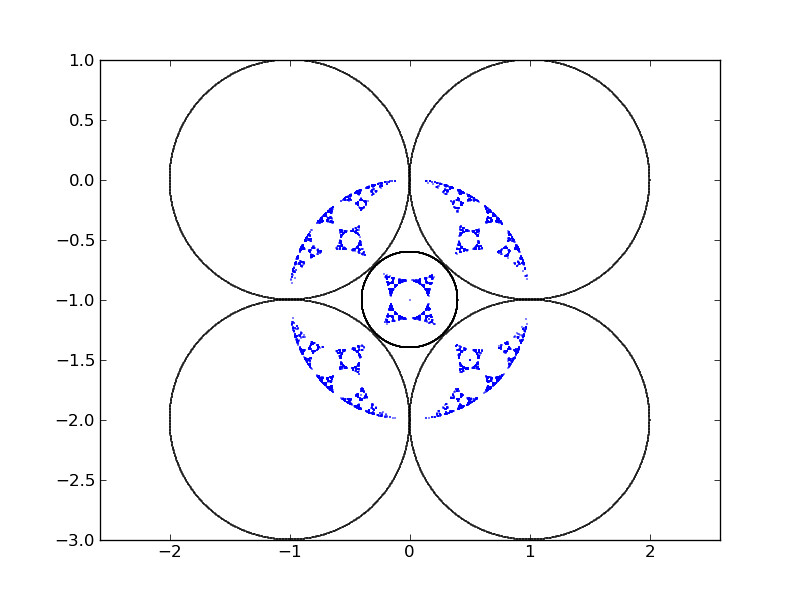
An IFS consisting on circle inversions with respect to five mutually disjoint disks

This is when the fun starts. Do the attractors for the circle inversion of these two examples with five disks look familiar?

Miscellaneous

The question is, how many disks, and which configuration must they observe so that the corresponding attractor is a proper Apollonian gasket? (a fractal generated from triples of circles, where each circle is tangent to the other two)

Let us go one step further, and allow in the IFS more general Möbius transformations. For example, a (modified) IFS with the three maps \( f_1, f_2 \) and \( f_3 \) defined below, offers a possible solution:

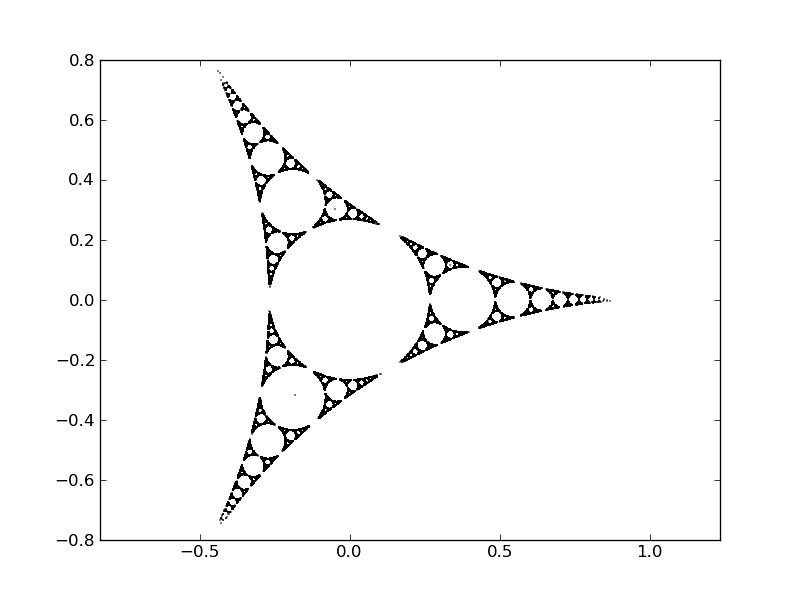
A naïve code to obtain this fractal is shown: Note that we have not included any mechanism to prevent any inversion to repeat itself in consecutive steps—that way we do not avoid having points that go back and forth through the same circle inversion.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
from numpy import *
import matplotlib.pyplot

def ifms(iterations):
    location=0+0*i
    X,Y=[],[]
    s=sqrt(3.0)

for step in range(iterations):
        location = 3/(1+s-location)-(1+s)/(2+s)
        choice=random.randint(3)
        if choice==1:
            location=f1*(-1+i*s)/2
        elif choice==2:
            location=f1*(-1-i*s)/2
        X.append(float32(location.real()))
        Y.append(float32(location.imag()))
    return X,Y

matplotlib.pyplot.figure()
matplotlib.pyplot.axis('equal')
X,Y=ifms(400000)
matplotlib.pyplot.plot(X,Y,'.k',ls='', markersize=1.0)
matplotlib.pyplot.savefig('/Users/blanco/Desktop/pointplot.png')