Bertrand Paradox

Classically, we define the probability of an event as the ratio of the favorable cases, over the number of all possible cases. Of course, these possible cases need to be all equally likely. This works great for discrete settings, like dice rolls, card games, etc. But when facing non-discrete cases, this definition needs to be revised, as the following example shows:

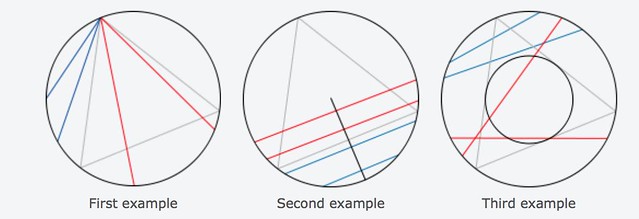
Consider an equilateral triangle inscribed in a circle. Suppose a chord of the circle is chosen at random. What is the probability that the chord is longer than a side of the triangle?

• Fix any point, say \( P \) in the circle. Consider any random chord in the circle, by choosing any other point \( Q \) on it. The number of possible cases is thus \( (2\pi \times 1)^2 = 4\pi^2. \) Place one of the vertices of the equilateral triangle on \( P \), and notice that the circle gets partitioned in three arcs with equal length \( ({2\pi}/{3}). \) Only if \( Q \) belongs in the arc farthest to \( P, \) we will have a chord longer than the side of the triangle. Therefore, the number of favorable cases is \( 2\pi \times \tfrac{2\pi}{3} = \tfrac{4\pi^2}{3}. \) Consequently, the probability we are looking for is \( \tfrac{1}{3}. \)
• Choose any point \( P \) on the circle, any point \( Q_P \) on the radius \( r_P=\overline{0P}, \) and consider the chord formed from the perpendicular to \( r_P \) by \( Q_P. \) There are \( 2\pi \times 1 = 2\pi \) possible cases. Place the equilateral triangle so that one of the sides is perpendicular to \( r_P, \) and notice that the number of favorable cases coincide with those chords where \( Q_P \) is nearer the center of the circle than the point where the side of the triangle intersects the radius. A simple trigonometric computation tells us that the number of favorable cases is precisely \( 2\pi \times \tfrac{1}{2} = \pi, \) and thus the probability we are looking for is \( \tfrac{1}{2}. \)
• Choose any point \( P \) in the interior of the disk, and consider the only chord that has \( P \) as a midpoint. There are \( \pi \times 1^2 = \pi \) possible cases. The chord will be longer than the side of the triangle, only if the chosen point falls within a concentric circle of radius \( \tfrac{1}{2}. \) The number of favorable cases is thus the area of this circle: \( \pi \times \big( \tfrac{1}{2} \big)^2 = \tfrac{\pi}{4}. \) The probability we are looking for is in this case \( \tfrac{1}{4}. \)

The three methods are sound: why did we get different answers? Which student do you think got it “right”? Can you explain what the paradox is in this situation?