Sequence of right triangles

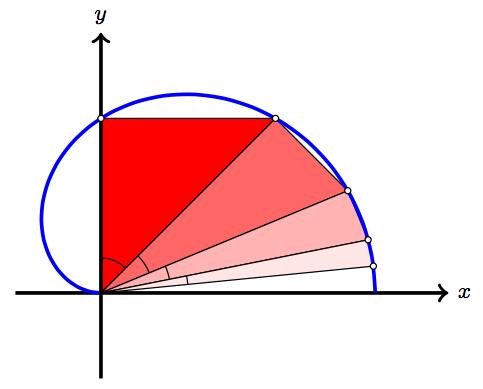
Consider the right triangle \(\triangle_1 \) with vertices at \((0,0) \), \((0,1) \), and \((1,1). \) Note that the angle at the origin is \(\frac{\pi}{4}. \) Use the hypotenuse of \(\triangle_1 \) as one of the legs of another right triangle, \(\triangle_2, \) with an angle of \(\frac{\pi}{8} \) at the origin, and whose second leg extends towards the \(x \)–axis. Continue constructing adjacent right triangles \(\triangle_n \) in the same fashion, with one leg supported on the hypothenuse of the previous right triangle \(\triangle_{n-1}, \) with angle \(\frac{\pi}{2^{n+1}} \) at the origin, and with a second leg extending towards the \(x \)–axis.

Note that, since the angles at the origin form the series \(\sum_{n=2}^\infty \frac{\pi}{2^n}, \) (that add up to \(\frac{\pi}{2} \)) the limit of the previous process is an actual segment on the \(x \)–axis.

What is the length of this segment?

Find an equation in polar coordinates \((\rho,\theta) \) of a curve passing through all the vertices of the resulting triangles, except possibly \((0,0). \)

Find an equation for that curve in rectangular coordinates.

Let us denote \( h_n \) the hypotenuse of triangle \( \triangle_n. \) By construction we have \( h_1=\sqrt{2} \) and, for each consecutive steps, the definition of cosine in our setup gives us that

\begin{equation} \cos \dfrac{\pi}{2^{n+1}} = \dfrac{h_{n-1}}{h_n}. \end{equation}

We may solve the recurrence with the aid of the formula of sine of double angles: \( \sin 2\alpha = 2 \sin \alpha \cos \alpha. \) In our case, setting \( \alpha = \frac{\pi}{2^{n+1}} \), we have

\begin{equation} \dfrac{h_{n-1}}{h_n} = \cos \dfrac{\pi}{2^{n+1}} = \dfrac{\sin \frac{\pi}{2^n}}{2\sin \frac{\pi}{2^{n+1}}} \end{equation}

or equivalently,

\begin{equation} h_n = \dfrac{2\sin \frac{\pi}{2^{n+1}}}{\sin \frac{\pi}{2^n}}\, h_{n-1} = \dfrac{2\sin \frac{\pi}{2^{n+1}}}{\sin \frac{\pi}{2^n}}\, \dfrac{2\sin \frac{\pi}{2^n}}{\sin \frac{\pi}{2^{n-1}}}\, h_{n-2} = \dotsb = 2^{n-1} \dfrac{\sin \frac{\pi}{2^{n+1}}}{\sin \frac{\pi}{2^2}} h_1 \end{equation}

which is the same as

\begin{equation} h_n = 2^n \sin \frac{\pi}{2^{n+1}} = \dfrac{\pi}{2}\, \dfrac{2^{n+1}}{\pi}\, \sin \frac{\pi}{2^{n+1}}. \end{equation}

We use this identity to obtain the answer to the first two questions. For instance, an expression in polar coordinates of a function that goes through all the vertices of the triangles could be given by

\begin{equation} \rho(\theta) = \dfrac{\pi}{2}\, \dfrac{\sin \theta}{\theta}. \end{equation}

And in that case, the length of the segment at the limit is given by

\begin{equation} \displaystyle{\lim_n h_n = \lim_{\theta\to 0} \rho(\theta) = \frac{\pi}{2}}. \end{equation}

I leave the third part of the puzzle an an exercise to the reader.

Miscellaneous

This is the \( \LaTeX \) code used with tikz to produce the diagram above. Note the power of the plot command, that allows us to obtain a very accurate graph of any function.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
\begin{tikzpicture}[scale=2]
 \draw[very thick,->] (-0.49,0) -- (1.99,0) node[right]{ $x$ };
  \draw[fill=red] (0,0) -- (0,1) -- (1,1) -- cycle;
  \draw[fill=red!60!white] (0,0) -- (22.5:1.5307) -- (1,1) -- cycle;
  \draw[fill=red!30!white] (0,0) -- (11.25:1.5607) -- (22.5:1.5307) -- cycle;
  \draw[fill=red!10!white] (0,0) -- (5.625:1.56827) -- (11.25:1.5607) -- cycle;
  \draw[domain=0.001:3.141,smooth,variable=\t,very thick,blue] %
      plot ({\t r}:1.570796*{sin(\t r)}/\t);
  \draw (90:0.2) arc (90:45:0.2);
  \draw (45:0.3) arc (45:22.5:0.3);
  \draw (22.5:0.4) arc (22.5:11.25:0.4);
  \draw (11.25:0.5) arc (11.25:5.625:0.5);
  \draw[very thick,->] (0,-0.49) -- (0,1.49) node[above]{ $y$ };
  \draw[fill=white] (0,1) circle (0.5pt);
  \draw[fill=white] (1,1) circle (0.5pt);
  \draw[fill=white] (22.5:1.5307) circle (0.5pt);
  \draw[fill=white] (11.25:1.5607) circle (0.5pt);
  \draw[fill=white] (5.625:1.56827) circle (0.5pt);
\end{tikzpicture}