What day of the week?

What day of the week was I born? Getting a calendar of that year could prove an impossible task, although if you are in front of a computer, there are *nix utilities that will do that for you. But seriously, who has access to a computer with unix or linux when the question pops?

There is a neat algorithm that, without the aid of pen and paper, will let you find the day of the week for any given date. It only takes six simple steps. On each of the first five steps, you come up with a different coefficient. In the last step, you add all those coefficients together and perform a very simple operation that offers a number between zero and six. This number indicates the day of the week:

\begin{equation} \underbrace{\text{August}}_{M} \underbrace{22^{\text{nd}}}_{D} \overbrace{\underbrace{19}_{C}\underbrace{73}_{Y}}^{L} \end{equation}

The CENTURY step.

The century coefficient, which we denote \( C \), is computed from the first two digits of the year. The coefficient for 20 is “minus one”, and for any other century, you can obtain the coefficient from the following table:

\begin{equation} \begin{array}{|c|c|c|c|c|c|c|c|} \hline\dotsc & 17 & 18 & 19 & 20 & 21 & 22 & \dotsc\\ \hline\dotsc & +4 & +2 & 0 & -1 & -3 & -5 & \dotsc\\ \hline\end{array} \end{equation}

For example, the first two digits of 1973 are 19: the corresponding coefficient is \( C=0. \)

The YEAR step.

The year coefficient, which we denote \( Y \), is computed from the last two digits of the year as the output of the following formula: if \( x \) is the last two digits of the year, then \( Y = x + \lfloor \frac{x}{4} \rfloor, \) where \( \lfloor \cdot \rfloor \) indicates the integer part of any given real number.

For example, the last two digits of 1973 are 73. Since \( 73 = 4 \times 18+3, \) the year coefficient is \( Y = 73 + 18 = 91.\)

The MONTH step.

This is the part that takes some memorizing. The month coefficient is given by the table below. Lewis Carroll gave a very nice rule to construct that table:

January is "zero"; February and March are both "three" (the third month); December is "twelve" (the twelfth month). For each month that starts or ends in a vowel, its month number subtracted from ten. For the next month to one of those, the previous coefficient plus the number of days of the previous month. \begin{equation} \begin{array}{|c|c|c|c|} \hline Jan & Feb & Mar & Apr\\ \hline 0 & 3 & 3 & 10-4=6\\ \hline\hline May & Jun & Jul & Aug\\ \hline 6+30=36 & 10-6=4 & 4+30=34 & 10-8=2\\ \hline\hline Sep & Oct & Nov & Dec\\ \hline 2+31=33 & 10-10=0 & 0+31=31 & 12\\ \hline \end{array} \end{equation}

For example, August has a two in the table. The month coefficient is thus \( M = 2.\)

The LEAP YEAR step.

Every year whose two last digits are a multiple of four is a leap year (except if those two digits are both zero—in that case, leap year occurs only if the whole year is a multiple of four-hundred). In case of leap year and the month being either January or February, we subtract one. Otherwise, zero.

For example, 1973 is not a leap year, so the coefficient is \( L=0.\)

The DAY step.

The corresponding coefficient \( D \), is simply the day of the month.

For August 22, the coefficient is \( D = 22.\)

Final Step.

In the final step, we add up all the previous coefficients, and compute the remainder after division by seven (this is equivalent to add or subtract seven as many times as necessary so we obtain a number between zero and six). This indicates the day of the week, by the easy correspondence Sunday is zero, Monday is one, and so on.

For example, for August 22, 1973, we have

\begin{equation} C + Y + M + L + D = 0 + 91 + 2 + 0 + 22 = 115 = 7 \times 16 + 3. \end{equation}

The remainder is thus 3, and the day of the week is Wednesday.

Miscellaneous

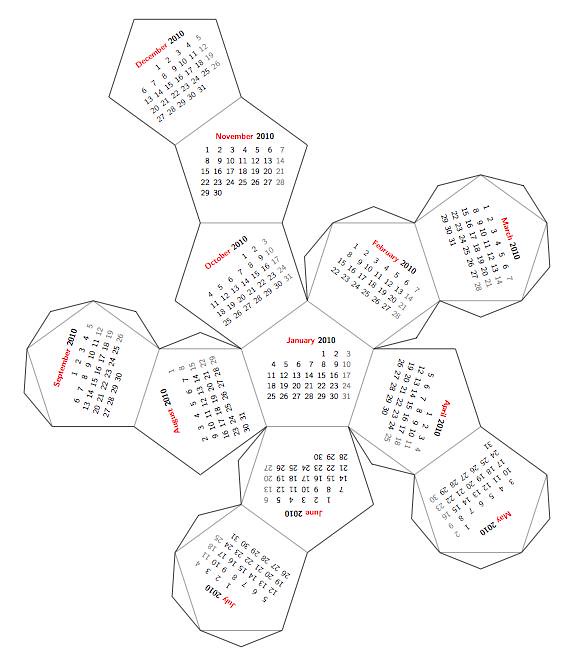
With the help of the libraries calendar and folding of the \( LaTeX \) package tikz, it is possible to generate this fun calendar printed on an unfolded dodecahedron. The code could not be simpler:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
\sffamily\scriptsize
\begin{center}
\begin{tikzpicture}[transform shape, 
    every calendar/.style= {at={(-8ex,4ex)}, week list, month label above centered, 
                            month text=\bfseries\textcolor{red}{\%mt} \%y0, 
                            if={(Sunday) [black!50]} }]

\tikzfoldingdodecahedron [folding line length=2.5cm,
  face 1={ \calendar [dates=\the\year-01-01 to \the\year-01-last];},
  face 2={ \calendar [dates=\the\year-02-01 to \the\year-02-last];},
  face 3={ \calendar [dates=\the\year-03-01 to \the\year-03-last];},
  face 4={ \calendar [dates=\the\year-04-01 to \the\year-04-last];},
  face 5={ \calendar [dates=\the\year-05-01 to \the\year-05-last];},
  face 6={ \calendar [dates=\the\year-06-01 to \the\year-06-last];},
  face 7={ \calendar [dates=\the\year-07-01 to \the\year-07-last];},
  face 8={ \calendar [dates=\the\year-08-01 to \the\year-08-last];},
  face 9={ \calendar [dates=\the\year-09-01 to \the\year-09-last];},
  face 10={\calendar [dates=\the\year-10-01 to \the\year-10-last];},
  face 11={\calendar [dates=\the\year-11-01 to \the\year-11-last];},
  face 12={\calendar [dates=\the\year-12-01 to \the\year-12-last];}
];

\end{tikzpicture}
\end{center}