A geometric fallacy

A geometric fallacy is basically a geometric construction that leads to a false result.  I once found an obscure russian treatise on this matter (published by мир), that kept me entertained for weeks: Ya.S.Dubnov’s Errores en las demostraciones geométricas.  The edition I have is a decent translation into Spanish, made by K.Medkov in 1993, although unfortunately some of the translated statements had to be treated with a grain of salt.  Nonetheless, I did enjoy greatly browsing through the different geometric problems, and learned quite a bit about mathematical reasoning.

Most of the geometric fallacies rely on the use of correct reasoning on the incorrect figures. But I would like to present here one of the most amusing ones, not only for the fact that it didn’t use a wrong figure, but also because it takes us to deliver a contradiction to the Pythagorean Theorem!  It goes like this:

In all right triangles, the sum of the lengths of the legs equals the length of the hypothenuse.  That is, the sides \( a \), \( b \) and \( c \) satisfy \( a+b=c \), where the largest side is conventionally denoted \( c \) and is called the hypotenuse.  The other two sides, of length \( a \) and \( b \) are called the legs (or the catheti)

(see the page in e.g. wikipedia for more information about triangles)

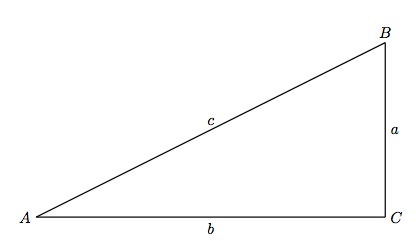
The “proof” of this absurd result is done by taking to the limit a clever construction.  Let us start with a given right triangle, and consider its two legs alone:

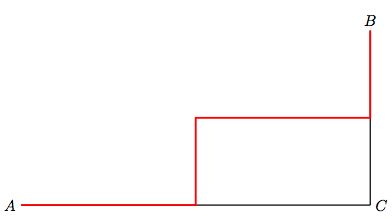
Starting in the vertex \( A \), consider a staircase of segments that goes through the midpoints of the sides of the triangle, until reaching the vertex \( B \). Notice that the lengths of segments of this staircase add up to \( a+b \) by construction.

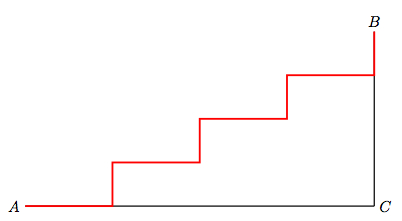Repeat the same staircase construction starting in the vertex \( A \), and using the midpoints of the previous staircase, until reaching vertex \( B \). The lengths of the segments of this new staircase still add up to \( a+b \).

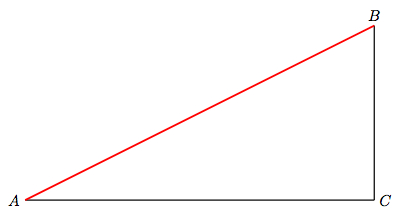By taking this construction to the limit, new staircases of length \( a+b \) are constructed that tend to the hypotenuse (in the sense that, after some iterations, the staircase and the hypotenuse will be as close to each other as desired).  We infere that the limit of these staircases is indeed the hypotenuse, and since the length of each staircase remained constant \( a+b \), the length of the hypotenuse must also be \( a+b \).

QED

This is obviously not true. What is wrong with this proof?