Mechanical Geometry Theorem Proving

In 1977, Professor Wen-Tsun Wu succeeded in developing a method of mechanical geometry theorem proving. This method has been applied to prove or even discover hundreds of non-trivial difficult theorems in elementary and differential geometries on a computer in an almost trivial manner. Usign Ritt’s differential algebra, Wu established a method for solving algebraic and differential equations by transforming an equation system in the general form to equation systems in triangular form. This is the Ritt-Wu decomposition algorithm, that later on was shown to be equivalent to perform a series of operations on ideals, very easily carried out by means of Gröbner basis manipulation.

I wrote a script in MAPLE to perform evaluations of the validity of some simple theorems in Euclidean Geometry, and wrote a small paper (in Spanish) on one of my findings, that was published in Bol. Asoc. Prof. Puig Adams, in October’99: “Sobre demostración automática de un problema geométrico”.

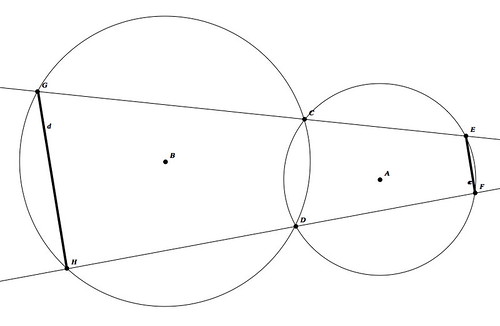
The example I cover in that short article can be seen below.

Given: Circles \( A \), \( B \) that intersect each other in points \( C \) and \( D \), and given points \( E \), \( F \) in circle \( A \), consider line \( a \) through \( E \) and \( C \), and line \( b \) through \( F \) and \( D \). The intersections of line \( a \) with circle \( A \) are \( C \) and \( G \). The intersections of line \( b \) with circle \( B \) are \( D \) and \( H \). Consider the segments \( c \) (connecting \( E \) with \( F \)) and \( d \) (connecting \( G \) with \( H \)).

To prove: Segments \( c \) and \( d \) are parallel.

Proposed Solution

Let us assume the points \( C \) and \( D \) have coordinates \( C=(0,1) \) and \( D=(0,-1) \), and the centers of the circles are \( A=(a,0) \), \( B=(b,0) \). Let us consider a vector \( \nu = (\nu_1, \nu_2) \) supported in the point \( C \), and a vector \( \omega = (\omega_1, \omega_2) \) supported in the point \( D \).

A line through \( C \) with leading vector \( \nu \) intersects the circle \( A \) at the point \( E=(x_1,y_1) \). In order to compute its coordinates, we consider the equations of the line and the circle:

\begin{equation} x_1 - \alpha \nu_1 = 0 \label{eq:1} \end{equation}

\begin{equation} y_1 - 1 - \alpha\nu_2 = 0 \label{eq:2} \end{equation}

\begin{equation*} (x_1-a)^2 + y_1^2 = 1+a^2 \end{equation*}

By simple substitution, we obtain the following second-degree equation, stating the condition:

\begin{equation*} (\nu_1^2 + \nu_2^2) \alpha^2 + 2(\nu_2 - \nu_1)\alpha = 0 \end{equation*}

One of the solutions is the trivial \( \alpha=0 \) (the point \( C \)). The other solution is what we need:

\begin{equation} (\nu_1^2 + \nu_2^2)\alpha + 2(\nu_2 - \nu_1) = 0 \label{eq:3} \end{equation}

Let \( g_1(x_1,\alpha) \), \( g_2(y_1,\alpha) \) and \( g_3(\alpha) \) be polynomials obtained from \( \eqref{eq:1}, \eqref{eq:2}, \eqref{eq:3}. \) We obtain polynomials \( g_4(x_2,\beta) \), \( g_5(y_2, \beta) \) and \( g_6(\beta) \) in a similar way, considering the condition of point \( F \) belonging in the line through \( D \) with leading vector \( \omega \) and the circle \( A \). We also obtain polynomials \( g_7(x_3, \gamma) \), \( g_8(y_3,\gamma) \) and \( g_9(\gamma) \) for the point \( G \) in circle \( B \) and line through \( C \) with leading vector \( \nu \). Finally, obtain polynomials \( g_{10}(x_4,\delta) \), \( g_{11}(y_4,\delta) \) and \( g_{12}(\delta) \) for point \( H \) belonging to circle \( B \) and the line through point \( D \) with leading vector \( \omega \).

We use the Ritt-Wu method on those polynomials (notice it is not necessary to turn the system in triangular, since by a simple re-ordering of the polynomials we accomplish this state). The proof follows:

\begin{align*} h_1 &= g_1 & h_5 &= g_7 & h_9 &= g_3 \\ h_2 &= g_2 & h_6 &= g_8 & h_{10} &= g_6 \\ h_3 &= g_3 & h_7 &= g_{10} & h_{11} &= g_9 \\ h_4 &= g_5 & h_8 &= g_{11} & h_{12} &= g_{12} \end{align*}

The degenerate conditions are then reduced to vectors \( \nu \) and \( \omega \) being not nill:

\begin{equation*} \nu_1^2 + \nu_2^2 \neq 0\qquad \omega_1^2+\omega_2^2 \neq 0 \end{equation*}