The following diagram shows a graph that represents a series of web pages (numbered from 1 to 8).

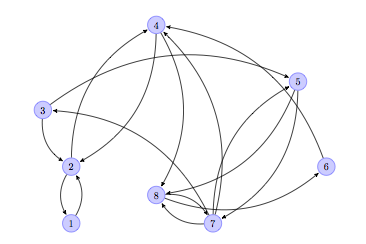
An arrow from a node to another indicates the existence of a link from the web page represented by the sending node, to the page represented by the receiving node. For example, the arrow from node 2 to node 1 indicates that there is a link in web page 2 pointing to web page 1. Notice how web page 4 has two outer links (to pages 2 and 8), and there are three pages that link to web page 4 (pages 2, 6 and 7). The pages represented by nodes 2, 4 and 8 seem to be the most popular at first sight.

Is there a mathematical way to actually express the popularity of a web page within a network? Researchers at Google came up with the idea of a PageRank to roughly estimate this concept by counting the number and quality of links to a page. It goes like this:

We construct a transition matrix of this graph \( T=\big( a_{i,j} \big) \) in the following fashion: the entry \( a_{i,j} \) is \( 1/k \) if there is a link from web page \( i \) to web page \( j \), and the total number of outer links in web page \( i \) amounts to \( k \). Otherwise, the entry is just zero. The size of a transition matrix of \( N \) web pages is always \( N \times N \). In our case, the matrix has size \( 8 \times 8 \):

\begin{equation} \begin{pmatrix} 0 & 1/2 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1/2 & 1/2 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1/3 & 0 \\ 0 & 1/2 & 0 & 0 & 0 & 1 & 1/3 & 0 \\ 0 & 0 & 1/2 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1/2\\ 0 & 0 & 0 & 0 & 1/2 & 0 & 0 & 1/2\\ 0 & 0 & 0 & 1/2 & 1/2 & 0 & 1/3 & 0 \end{pmatrix} \end{equation}

Let us open an ipython session and load this particular matrix to memory. Remember that in python, indices start from zero, not one:

import numpy as np, matplotlib.pyplot as plt, scipy.linalg as spla, scipy.sparse as spsp, scipy.sparse.linalg as spspla

np.set_printoptions(suppress=True, precision=3)

cols = np.array([0,1,1,2,2,3,3,4,4,5,6,6,6,7,7])
rows = np.array([1,0,3,1,4,1,7,6,7,3,2,3,7,5,6])
data = np.array([1., 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 1., 1./3, 1./3, 1./3, 0.5, 0.5])

T = np.zeros((8,8)) 
T[rows,cols] = data

From the transition matrix, we create a Page Rank matrix, \( G \) (also known as the Google matrix), by fixing a positive constant \( 0 < p \leq 1 \), and following the formula \( G = (1-p) \cdot T + p \cdot B \). Here, \( B \) is a matrix with the same size as \( T \), with all its entries equal to \( 1/N \). For example, if we choose \( p=0.15 \), we obtain the following Google matrix

G = (1-0.15) * T + 0.15/8

print G

[[ 0.019  0.444  0.019  0.019  0.019  0.019  0.019  0.019]
 [ 0.869  0.019  0.444  0.444  0.019  0.019  0.019  0.019]
 [ 0.019  0.019  0.019  0.019  0.019  0.019  0.302  0.019]
 [ 0.019  0.444  0.019  0.019  0.019  0.869  0.302  0.019]
 [ 0.019  0.019  0.444  0.019  0.019  0.019  0.019  0.019]
 [ 0.019  0.019  0.019  0.019  0.019  0.019  0.019  0.444]
 [ 0.019  0.019  0.019  0.019  0.444  0.019  0.019  0.444]
 [ 0.019  0.019  0.019  0.444  0.444  0.019  0.302  0.019]]
 

Google matrices have some interesting properties:

• 1 is an eigenvalue of multiplicity one.
• 1 is actually the largest eigenvalue: all the other eigenvalues are in modulus smaller than 1.
• The eigenvector corresponding to eigenvalue 1 has all entries positive. In particular, for the eigenvalue 1 there exists a unique eigenvector with the sum of its entries equal to one. This is what we call the Page Rank vector.

A quick computation with scipy.linalg.eig finds that eigenvector for us:

eigenvalues, eigenvectors = spla.eig(G)

print eigenvalues

[ 1.000+0.j    -0.655+0.j    -0.333+0.313j -0.333-0.313j -0.171+0.372j
 -0.171-0.372j  0.544+0.j     0.268+0.j   ]
 

PageRank = eigenvectors[:,0]
PageRank /= sum(PageRank)

print PageRank.real

[ 0.117  0.232  0.048  0.219  0.039  0.086  0.102  0.157]

Those values correspond to the Page Ranks of each of the eight web pages depicted on the graph. As expected, the maximum value of those is associated to the second web page (0.232), closely followed by the fourth (0.219), and then the eighth web page (0.157).

Note how this problem of networks of web pages has been translated into mathematical objects, to an equivalent problem involving matrices, eigenvalues and eigenvectors, and has been solved with techniques of Linear Algebra.

The transition matrix is sparse: most of its entries are zeros. Sparse matrices with extremely large size are of special importance in Numerical Linear Algebra, not only because they encode challenging scientific problems, but also because it is extremely hard to manipulate them with basic algorithms.

Rather than storing to memory all values in the matrix, it makes sense to collect only the non-zero values instead, and use algorithms with exploit these smart storage schemes. The gain in memory management is obvious. These methods are usually faster for this kind of matrices and give less roundoff errors, since there are usually far less operations involved. This is another advantage of scipy, since it contains numerous procedures to attack different problems where data is stored in this fashion. Let us observe its power with another example:

The University of Florida Sparse Matrix Collection is the largest database of matrices accessible online. As of January 2014, it contains 157 groups of matrices arising from all sorts of scientific disciplines. The sizes of the matrices range from very small (1-by-2) to insanely large (28-million-by-28-million). More matrices are expected to be added constantly, as they arise in different engineering problems.

More information about this database can be found in ACM Transactions on Mathematical Software, vol 38, Issue 1, 2011, pp 1:1 - 1:25, by T.A. Davis and Y.Hu, or online at www.cise.ufl.edu/research/sparse/matrices

For example, the group with the most matrices in the database is the original Harwell-Boeing Collection, with 292 different sparse matrices. This group can also be accessed online at the Matrix Market: math.nist.gov/MatrixMarket

Each matrix in the database comes in three formats:

• Matrix Market Exchange Format [Boisvert et al. 1997]
• Rutherford-Boeing Exchange Format [Duff et al. 1997]
• Proprietary matlab .mat format

Let us import to our ipython session two matrices in Matrix Market Exchange format from the Collection, meant to be used in a solution of a least squares problem. These matrices are located at www.cise.ufl.edu/research/sparse/matrices/Bydder/mri2.html

We download the corresponding tar bundle and untar it to get two ASCII files:

• mri2.mtx (the main matrix in the least squares problem)
• mri2_b.mtx (the right-hand side of the equation)

The first twenty lines of the file mri2.mtx read as follows:

%% MatrixMarket matrix coordinate real general
%-----------------------------------------------------------------
% UF Sparse Matrix Collection, Tim Davis
% http://www.cise.ufl.edu/research/sparse/matrices/Bydder/mri2
% name: Bydder/mri2
% [MRI reconstruction (2), from Mark Bydder, UCSD]
% id: 1318
% date: 2005
% author: M. Bydder
% ed: T. Davis
% fields: title A name b id notes date author ed kind
% kind: computer graphics/vision problem
%-----------------------------------------------------------------
% notes:
% x=lsqr(A,b); imagesc(abs(fftshift(fft2(reshape(x,384,384)))));
%-----------------------------------------------------------------
63240 147456 569160
31992 1720 .053336731395584265
31992 1721 .15785917688901102
31992 1722 .07903055194318191

The first sixteen lines are comments, and give us some information about the generation of the matrix.

• The computer vision problem where it arose: An MRI reconstruction.
• Author information: Mark Bydder, UCSD.
• Procedures to apply to the data: Solve a least square problem \( A x - b \), and posterior visualization of the result.

The seventeenth line indicates the size of the matrix: 63240 rows by 147456 columns, as well as the number of non-zero entries in the data: 569160.

The rest of the file includes precisely 569160 lines, each containing two integer numbers, and a floating point number: These are the locations of the non-zero elements in the matrix, together with the corresponding values.

We need to take into account that these files use the Fortran convention of starting arrays from 1, not from 0.

A good way to read this file into an ndarray is by means of the function loadtxt in numpy. We can then use scipy to transform the array into a sparse matrix with the function coo_matrix in the module scipy.sparse (coo stands for coordinate internal format).

rows, cols, data = np.loadtxt("mri2.mtx", skiprows=17, unpack=True)
rows -= 1 
cols -= 1

MRI2 = spsp.coo_matrix((data, (rows, cols)), shape=(63240,147456))

The best way to visualize the sparsity of this matrix is by means of the routine spy from the module matplotlib.pyplot.

These are the first ten lines from the second file, mri2_b.mtx, which does not represent a sparse matrix, but a column vector:

$ head mri2_b.mtx

%%MatrixMarket matrix array complex general
%-------------------------------------------------------------------------------
% UF Sparse Matrix Collection, Tim Davis
% http://www.cise.ufl.edu/research/sparse/matrices/Bydder/mri2
% name: Bydder/mri2 : b matrix
%-------------------------------------------------------------------------------
63240 1
-.07214859127998352 .037707749754190445
-.0729086771607399 .03763720765709877
-.07373382151126862 .03766685724258423

Those are six commented lines with information, one more line indicating the shape of the vector (63240 rows and one column), and the rest of the lines contain two columns of floating point values: the real and imaginary parts of the corresponding data. We proceed to read this vector to memory, solve the least squares problem suggested, and obtain the following reconstruction:

r_vals, i_vals = np.loadtxt("mri2_b.mtx", skiprows=7, unpack=True)

%time solution = spspla.lsqr(MRI2, r_vals + 1j*i_vals)

CPU times: user 5min, sys: 1min 49s, total: 6min 49s
Wall time: 6min 50s

from scipy.fftpack import fft2, fftshift

img = solution[0].reshape(384,384)
img = np.abs(fftshift(fft2(img)))
plt.figure(figsize=(8,8))
plt.imshow(img)

<matplotlib.image.AxesImage at 0x11218c250>

If interested in the theory behind the creation of this matrix and the particulars of this problem, read the article On the optimality of the Gridding Reconstruction Algorithm, by H. Sedarat and D. G. Nishimura, published in IEEE Trans. Medical Imaging, vol 19, no 4, pp. 306-317, 2000.

For matrices with a good structure, which are going to be exclusively involved in matrix multiplications, it is often possible to store the objects without allocating almost any space. Consider the following example:

A horizontal earthquake oscillation affects each floor of a tall building, depending on the natural frequencies of oscillation of the floors. If we make certain assumptions, a model to quantize the oscillations on buildings with N floors can be obtained as a second-order system of N differential equations by competition: the Newton’s second law force is set equal to the sum of Hooke’s forces, and the external force due to the earthquake wave.

These are the assumptions we need:

• Each floor is considered a point of mass located at its center-of-mass. The floors have masses \( m_1, m_2, …, m_N \).
• Each floor is restored to its equilibrium position by a linear restoring force (Hooke’s \( -k \times \text{elongation} \)). The Hooke’s constants for the floors are \( k_1, k_2, …, k_N \).
• The locations of masses representing the oscillation of the floors are \( x_1, x_2, …, x_N \). We assume all of them functions of time, and that at equilibrium they are all equal to zero.
• For simplicity of exposition, we are going to assume no friction: all damping effects on the floors are ignored.
• The equations of a floor depend only on the neighboring floors.

Set \( M \), the mass matrix, to be a diagonal matrix containing the floor masses on its diagonal. Set \( K \), the Hooke’s matrix, to be a tri-diagonal matrix with the following structure: for each row \( j \), all the entries are zero except

• Column \( j-1 \), which we set to be \( k_{j+1} \),
• Column \( j \), which we set to \( -k_{j+1}-k_j \), and
• Column \( j+1 \), which we set to \( k_{j+2} \).

Set \( H \) to be a column vector containing the external force on each floor due to the earthquake, and \( X \) the column vector containing the functions \( x_j \).

We have then the system \( M \cdot X^{\prime\prime} = K \cdot X + H \). The Homogeneous part of this system is the product of the inverse of \( M \) with \( K \), which we denote \( A \).

To solve the homogeneous linear second-order system \( X^{\prime\prime} = A \cdot X \), we define the variable \( Y \) to contain \( 2N \) entries: all \( N \) functions \( x_j \), followed by their derivatives \( x^\prime_j \). Any solution of this second-order linear system has a corresponding solution on the first-order linear system \( Y^\prime = C \cdot Y \), where \( C \) is a block matrix of size \( 2N \times 2N \). This matrix \( C \) is composed by a block of size \( N \times N \) containing only zeros, followed horizontally by the identity (of size \( N \times N \)), and below these two, the matrix \( A \) followed horizontally by another \( N \times N \) block of zeros.

It is not necessary to store this matrix \( C \) into memory, or any of its factors or blocks. Instead, we will make use of its structure, and use a Linear Operator to represent it. Minimal data is then needed to generate this operator (only the values of the masses and the Hooke’s coefficients): much less than any matrix representation of it.

Let us show a concrete example with 6 floors. We indicate first their masses and Hooke’s constants, and proceed to construct a representation of \( A \) as a linear operator:

m = np.array([56., 56., 56., 54., 54., 53.])
k = np.array([561., 562., 560., 541., 542., 530.])

def Axv(v):
    global k, m
    w = v.copy()
    w[0] = (k[1]*v[1] - (k[0]+k[1])*v[0])/m[0]
    for j in range(1, len(v)-1):
        w[j] = k[j]*v[j-1] + k[j+1]*v[j+1] - (k[j]+k[j+1])*v[j]
        w[j] /= m[j]
    w[-1] = k[-1]*(v[-2]-v[-1])/m[-1]
    return w

A = spspla.LinearOperator((6,6), matvec=Axv, matmat=Axv, dtype=np.float64)

The construction of \( C \) is very simple now (much simpler than its matrix!):

def Cxv(v):
    n = len(v)/2
    w = v.copy()
    w[:n] = v[n:]
    w[n:] = A * v[:n]
    return w

C = spspla.LinearOperator((12,12), matvec=Cxv, matmat=Cxv, dtype=np.float64)

A solution of this homogeneous system comes in the form of an action of the exponential of \( C \): \( Y(t) = \operatorname{expm}(C t) \cdot Y(0) \), where \( \operatorname{expm}() \) here denotes a matrix exponential function. In scipy, this operation is performed with the routine expm_multiply in the module scipy.sparse.linalg.

For example, in our case, given the initial value containing the values \( x_1(0)=0, \dots, x_N(0)=0, x^\prime_1(0)=1, \dots, x^\prime_N(0)=1 \), if we require a solution \( Y(t) \) for values of \( t \) between 0 and 1 in steps of size 0.1, we could issue the following:

initial_condition = np.zeros(12)
initial_condition[6:] = 1

Y = spspla.expm_multiply(C.matmat(np.eye(12)), np.ones(12), start=0, stop=1, num=10)

It has been reported in some installations that, in the next step, a matrix for \( C \) must be given instead of the actual linear operator (thus contradicting the manual). If this is the case in your system, simply change \( C \) in the next lines, to its matrix representation.

The oscillations of the six floors during the first second can then be calculated and plotted as follows.

plt.figure(figsize=(8,8))
plt.plot(np.linspace(0,1,10), Y[:,:6])
plt.xlabel('time (in seconds)')
plt.ylabel('oscillation')
plt.legend(np.arange(6)+1, loc=2)

<matplotlib.legend.Legend at 0x10a28bd90>

For more details about systems of differential equations, and how to solve them with actions of exponentials, read for example the excellent book Elementary Differential Equations 10 ed., by William E. Boyce and Richard C. DiPrima. Wiley, 2012.

These three examples illustrate the goal of this first chapter: Numerical Linear Algebra. In python this is accomplished first by storing the data in matrix form, or as a related linear operator, by means of any of the following classes:

• numpy.ndarray (making sure that they are two-dimensional)
• numpy.matrix
• scipy.sparse.bsr_matrix (Block Sparse Row matrix)
• scipy.sparse.coo_matrix (Sparse Matrix in COOrdinate format)
• scipy.sparse.csc_matrix (Compressed Sparse Column matrix)
• scipy.sparse.csr_matrix (Compressed Sparse Row matrix)
• scipy.sparse.dia_matrix (Sparse matrix with DIAgonal storage)
• scipy.sparse.dok_matrix (Sparse matrix based on a Dictionary of Keys)
• scipy.sparse.lil_matrix (Sparse matrix based on a linked list)
• scipy.sparse.linalg.LinearOperator

As we have seen in the examples, the choice of different classes obeys mainly to the sparsity of the data, and the algorithms we are to apply on them.

This choice then dictates the modules that we use for the different algorithms: scipy.linalg for generic matrices, and both scipy.sparse, scipy.sparse.linalg, for sparse matrices or linear operators. These three scipy modules are compiled on top of the highly optimized computer libraries BLAS (written in Fortran77), LAPACK (in Fortran90), ARPACK (in Fortran77), and SuperLU (in C).

For a better understanding of these underlying packages, read the description and documentation from their creators:

• BLAS: netlib.org/blas/faq.html
• LAPACK: netlib.org/lapack/lapack-3.2.html
• ARPACK: www.caam.rice.edu/software/ARPACK/
• SuperLU: crd-legacy.lbl.gov/~xiaoye/SuperLU/

Most of the routines in these three scipy modules are wrappers to functions in the mentioned libraries. If we so desire, we also have the possibility to call the underlying functions directly. In the module scipy.linalg, we have

• scipy.linalg.get_blas_funcs to call routines from BLAS.
• scipy.linalg.get_lapack_funcs to call routines from LAPACK.

For example, if we want to use the BLAS function NRM2 to compute Frobenius norms:

blas_norm = spla.get_blas_funcs('nrm2')

blas_norm(np.float32([1e20]))

1.0000000200408773e+20

Notebook

For an ipython notebook with the current draft of chapter 1 (Numerical Linear Algebra) of my upcoming book Mastering Scipy, follow [this link] to the repository Mastering Scipy in my github.