Basic, Intermediate and CAS problems

The following is the list of non-advanced problems for Chapter 1 of the class notes. There is a forum open at the end, so you can ask questions. It is a great way to interact with the instructor and with other students in your class, should you need some assistance with any question. Please, do not post solutions.

1. Find and sketch the domain of the following functions.

   • \( f(x,y) = \sqrt{y-x-2} \)
   • \( f(x,y) = \log \big( x^2+y^2-4 \big) \)
   • \( f(x,y) = \dfrac{(x-1)(y+2)}{(y-x)(y-x^3)} \)
   • \( f(x,y) = \log (xy+x-y-1) \)

2. Find and sketch the level lines \( f(x,y)=c \) on the same set of coordinate axes for the given values of \( c \).

   • \( f(x,y) = x+y-1, c \in \{ -3, -2, -1, 0, 1, 2, 3 \}. \)
   • \( f(x,y) = x^2+y^2, c \in \{ 0, 1, 4, 9, 16, 25 \}. \)
   • \( f(x,y) = xy, c \in \{ -9, -4, -1, 0, 1, 4, 9 \}. \)

3. Use a Computer Algebra System of your choice to produce contour plots of the given functions on the given domains.

   • \( f(x,y) = (\cos x)(\cos y) e^{-\sqrt{x^2+y^2}/4} \) on \( [-2\pi, 2\pi] \times [-2\pi, 2\pi]. \)
   • \( g(x,y) = \dfrac{xy(x^2-y^2)}{x^2+y^2} \) on \( [-1,1] \times [-1,1]. \)
   • \( h(x,y) = y^2 - y^4 -x^2 \) on \( [-1,1]\times[-1,1] \).
   • \( k(x,y) = e^{-y}\cos x \) on \( [-2\pi, 2\pi]\times[-2,0]. \)
   

   
   

   

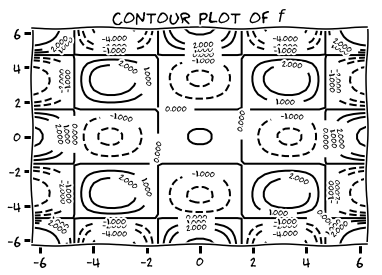
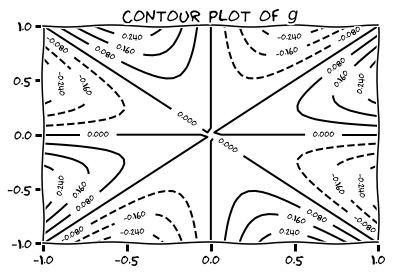
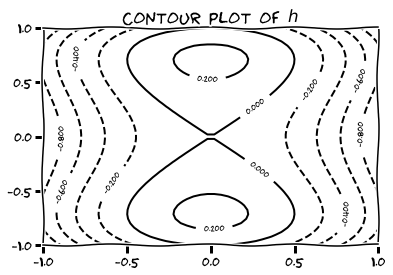
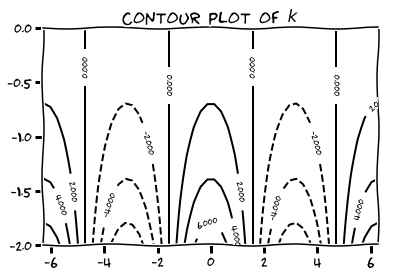
4. Sketch the curve \( f(x,y)=c \) together with \( \nabla f \) and the tangent line at the given point \( P \). Write an equation for the tangent line.

   • \( f(x,y)=x^2+y^2, c=4, P=(\sqrt{2}, \sqrt{2}). \)
   • \( f(x,y)=x^2-y, c=1, P=(\sqrt{2}, 1). \)
   • \( f(x,y)=xy, c=-1, P=(2, -1/2). \)
   • \( f(x,y)=x^2-xy+y^2, c=7, P=(-1,2). \)
5. For the function \( f(x,y) = \dfrac{x-y}{x+y} \) at the point \( P_0 = (-1/2, 3/2) \), find the directions \( \boldsymbol{v} \) and the directional derivatives \( D_{\boldsymbol{v}}f(P_0) \) for which
   • \( D_{\boldsymbol{v}}f(P_0) \) is largest.
   • \( D_{\boldsymbol{v}}f(P_0) \) is smallest.
   • \( D_{\boldsymbol{v}}f(P_0) = 0. \)
   • \( D_{\boldsymbol{v}}f(P_0) = 1. \)
   • \( D_{\boldsymbol{v}}f(P_0) = -2. \)

6. The derivative of \( f(x,y) \) at \( (1,2) \) in the direction \( \frac{\sqrt{2}}{2}[1,1] \) is \( 2\sqrt{2} \) and in the direction \( [0,-1] \) is \( -3 \). What is the derivative of \( f \) in the direction \( \frac{\sqrt{5}}{5}[-1,-2] \)?

7. Find the absolute maxima and minima of the function \( f(x,y) = (4x-x^2)\cos y \) on the rectangular plate \( 1\leq x \leq 3, -\frac{\pi}{4} \leq y \leq \frac{\pi}{4}. \)

8. Find two numbers \( a \leq b \) such that \( \int_a^b (24-2x-x^2)^{1/3}\, dx \) has its largest value.

9. Find the points of the hyperbolic cylinder \( x^2-z^2-1=0 \) in \( \mathbb{R}^3 \) that are closest to the origin.

10. Find the extreme values of the function \( f(x,y,z)=xy+z^2 \) on the circle in which the plane \( y-x=0 \) intersects the sphere \( x^2+y^2+z^2=4. \)

11. Write a routine (in your favorite CAS) that uses symbolic computation to find the minimum of a differentiable real-valued function \( f \colon \mathbb{R} \to \mathbb{R} \) over

    • a closed interval \( [a,b] \)
    • An interval of the form \( [a,\infty) \), or \( (-\infty, b] \)

    The routine should accept as input:

    • the expression of the function \( f \),
    • the endpoints \( a,b. \)