MATH 141 Summer E Session

Section 002

Instructor: Francisco Blanco-Silva

e-mail: blanco at math dot sc dot edu
phone: 777-0283
Office: LeConte 314D

Teaching Assistant: Christopher David Edgar

e-mail: edgarc at mailbox dot sc dot edu
phone: 777-7411
Office: LeConte 103A

Lab Assistant: Xiaofei Yi

e-mail: xyi at mailbox dot sc dot edu
phone: 777-7506
Office: LeConte 314A

Meeting Times and Office Hours

Morning Session: MTWThF  8:30 AM - 10:30 AM Petigru 217
Computer Labs: TTh  2:50 PM -  4:20 PM LeConte 102
Evening Sessionns: MWF  2:50 PM -  4:05 PM LeConte 412
Office Hours: Francisco MTWThF 10:30 AM - 11:59 AM LeConte 314D
Christopher MWF  4:30 PM -  5:30 PM LeConte 103A
Xiaofei TTh  4:30 PM -  5:50 PM LeConte 314A

Important deadlines you need to know

The Summer E session begins Monday, June 1st, and ends Saturday, June 27th. The last day to obtain a “W” grade or to elect a pass/fail grade is Saturday, June 13th. The first day in which a “WF” grade is assigned is therefore Sunday, June 14th.

Prerequisites

Qualifications earned by grade of C or better in MATH 112, 115, 116 or by a PreCalculus Placement Test.

Text

Calculus. Early Transcendentals by James Stewart. Thompson Brooks/Cole 2008 (sixth edition)

Student Solutions Manual for Stewart's Multivariable Calculus, 6th Edition Calculus: Early Transcendentals (Stewart's Calculus Series)

You will be required to use Enhanced WebAssign, the online homework system that accompanies your textbook, for my course. If you choose to purchase a hard copy of the textbook, you need to buy the bundle that comes with the Enhanced WebAssign code.

Course Structure and Grading Policies

Your final score for the course will be computed as follows:

  • Quizzes: (up to 100 points) 10% of the course grade.
    Five quizzes have been assigned online in WebAssign, to test your abilities and skills. Each quiz has a deadline as indicated in Lesson Plan below. In order to sign up for your section of the course on WebAssign, visit www.webassign.net and click on [Enter Class Key]. The class key is

    sc 8294 7968

    Click [here] to retrieve further registration instructions.
  • Computer Labs: (up to 100 points) 10% of the course grade.
  • Midterm Exams: (up to 100 points each) 60% of the course grade (15% each midterm).
    There will be four in-class midterm exams scheduled as follows:
    Test # Date
    1 Thu, Jun 04
    2 Tue, Jan 09
    3 Mon, Jan 15
    4 Mon, Jan 22
  • Final Exam: (up to 100 points) 20% of the course grade.
    The final exams is scheduled on Friday, June 26th, 2015 from 8:30 AM to 11:00 AM.

The course grade will be determined as follows:

GRADE RANGE
A 90%-100%
B+ 85%-89%
B 80%-84%
C+ 75%-79%
C 70%-74%
D+ 65%-69%
D 60%-64%
F below 60%

Further Information

  • Honor Code:
    The Honor Code applies to all work for this course. Please review the Honor Code at [this link]. Students found violating the Honor Code will be subject to discipline.
  • Some material will be stored in Dropbox. In that case, you will need an account to retrieve it. If you do not have one already, sign-in through [this link] with your academic e-mail address to receive a base 4GB storage, plus an extra 500MB, free of charge.
  • Remember to change your e-mail address on Blackboard if necessary [blackboard.sc.edu]
  • Office of Student Disability Services:
    If you have special needs as addressed by the Americans with Disabilities Act and need any assistance, please notify the instructor immediately.
  • Math Tutoring Center:
    The Math Tutoring center will be open Monday through Friday from 10:00 AM to 1:00 PM.

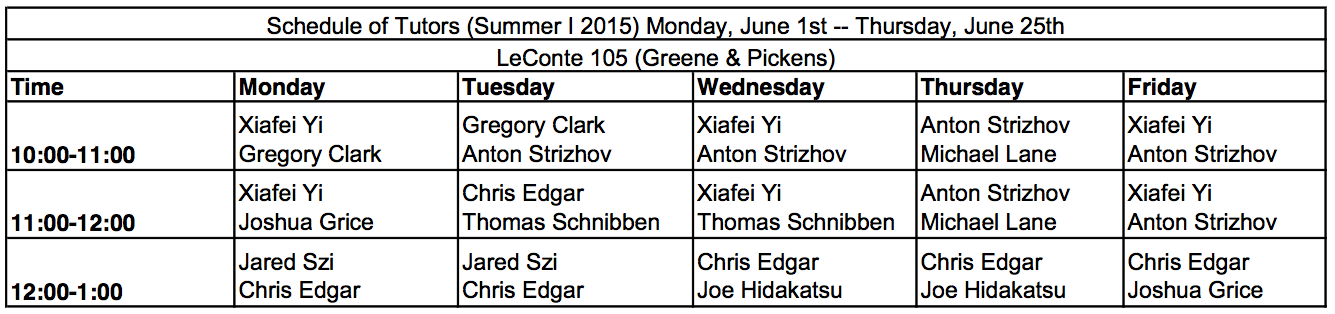
Learning Outcomes

A student who successfully completes Calculus I (MATH 141) should continue to develop as an independent learner with the ability to approach problems from a conceptual viewpoint, to utilize more than one idea in a single problem, and to apply appropriate calculus skills to problems in context. In particular, the successful student will master concepts and gain skills needed to solve problems related to:

  • Handling Functions
    • Functions: domain, range and graphs
    • Finding limits graphically, numerically and analytically
    • Continuity and one-sided limits
    • Infinite limits and limits at infinity
  • Differentiation
    • The derivative and rates of change
    • Basic differentiation rules
      • Polynomials
      • Exponentials
      • Trigonometric functions
      • Logarithmic functions
      • The product and quotient rule
      • Chain rule
    • Implicit differentiation
    • Logarithmic differentiation
  • Applications of differentiation
    • Extrema on an interval
    • Mean Value Theorem
    • Curve sketching
    • L'Hospital's Rule
    • Related rates
    • Optimization problems
  • Integration
    • Antiderivatives and indeterminate integrals
    • Definite Integrals
    • The Fundamental Theorem of Calculus
    • Basic computation of area between curves
    • Basic computation of volume of solids of revolution

Lesson plan

  • First part: Functions
    • Mon Jun 01: 1.2, 1.5 and 1.6: Intro to Functions. Exponential and Logarithmic Functions
      [pp.20--22: 1abcde, 2abcef, 5, 6, 7, 27, 28, 30, 38, 41, 42; p.58: 3, 4, 7, 8, 9, 10, 15, 17, 18; p.71: 33--39, 47--52]
    • Tue Jun 02: 1.3: New functions from old functions
      [pp.43--44: 1, 2, 3, 4, 5, 31, 32, 33, 34, 35, 36, 37, 38, 41, 42]
    • Wed Jun 03: 2.2, 2.3 and 2.5: Limits and Continuity
      [p.97: 4, 5, 6, 25, 26, 27, 29, 32, 34a. p.106: 1, 3--9, 11--27; pp.128: 3a, 4, 10--13, 16--18, 20, 35, 37, 39, 41, 42]
      [Quiz #1 due today]
    • Thu Jun 04: First Midterm---sections 1.2, 1.3, 1.5, 1.6, 2.2, 2.3, and 2.5
  • Second Part: Introduction to Differentiation
    • Fri Jun 05: Intro to derivatives:
      2.7 and 2.8: Definition, usage [p.150 :4ab, 5--8, 10ab, 21, 25--30]
      3.1: Derivatives of Polynomials and Exponential functions [p.180: 3--30, 33, 34, 45, 52, 53, 54]
      3.3: Derivatives of Trigonometric functions [p.195: 1--6, 9--14, 21, 23, 24, 25a, 34]
      3.6: Derivatives of Logarithmic functions [p.220: 2--22, 27--30, 33, 34, 37--50]
    • Mon Jun 08:
      3.2, 3.4. 3.5 and 3.6: Product, Quotient and Chain Rules. Implicit and Logarithmic differentiation
      [p.187: 1, 2, 7, 8, 9, 10, 11, 13, 14, 15, 16, 19, 21, 22, 26, 29, 31, 52; p.203: 1---21, 23, 25--30, 32--34, 36, 37, 51--54, 62; p.213: 1--30, 63, 64a, 65, 66]
      [Quiz #2 due today]
    • Tue Jan 09: Second Midterm---sections 2.7, 2.8, 3.1, 3.2, 3.3, 3.4, 3.5 and 3.6
  • Third Part: Applications of Differentiation
    • Wed Jan 10: 4.1, 4.2 and 4.3: Maximum and Minimum values. First and Second Derivative Test. The Mean Value Theorem.
      [p.277: 6, 8, 10, 29--44, 47--62; p.295: 5, 6, 7, 9--22, 33--50]
    • Thu Jun 11: 4.4: L'Hopital's Rule
      [p.304: 5--64]
    • Fri Jun 12: 4.5: Curve Sketching
      [p.314: 1--27]
      [Quiz #3 due today]
    • Mon Jan 15: Third Midterm---sections 4.1, 4.2, 4.3, 4.4, and 4.5
    • Tue Jan 16: 3.9: Related Rates I
      [p.245: 1--33]
    • Wed Jan 17: 3.9: Related Rates II. 4.7 Optimization Problems I
      [Quiz #4 due today]
    • Thu Jan 18: 4.7: Optimization Problems II
      [Quiz #5 due today]
    • Mon Jan 22: Fourth Midterm---sections 3.9, and 4.7
  • Fourth Part: Introduction to Integration
    • Tue Jun 23: 4.9 and 5.4: Antiderivatives and indefinite integrals
      [p.345: 1--15, 18, 18, 21; p.397: 5--18]
    • Wed Jun 24: Appendix E, 5.1 and 5.2: Sigma notation. Intro to Definite Integrals
      [p.A38: 1--36, 43--46]
    • Thu Jun 25: 5.3: The Fundamental Theorem of Calculus
      [p.388: 7--12, 19--33, 35, 36, 39, 40, 65, 66, 68, 74]