Given two topological spaces, \( (X,T_X) \) and \( (Y,T_Y), \) we say that a map \( \varphi \colon X \to Y \) is a homeomorphism if it satisfies the three properties below:
- It is a bijection (that is, both injective and surjective),
- it is continuous, and
- it has a continuous inverse \( \varphi^{-1} \colon Y \to X. \)
Two spaces for which there is such a homeomorphism are called homeomorphic. As it turns out, homeomorphic spaces have the same topological properties.
In what follows, we will construct several interesting homeomorphisms to train our skills:
Disks and squares
Consider the unit disk \( D_2 \) and the unit square \( \square_2 \) defined by
\begin{equation}
\begin{array}{l} D_2 = \{ x=(x_1,x_2) \in \mathbb{R}^2 : x_1^2 + x_2^2 \leq 1 \} \\ \square_2 =\{ x=(x_1,x_2) \in \mathbb{R}^2 : \lvert x_1 \rvert \leq 1, \lvert x_2 \rvert \leq 1 \} \end{array}
\end{equation}
We construct a homeomorphism \( \varphi \colon \square_2 \to D_2 \) as follows:
\begin{equation}
\varphi(x_1,x_2) = \begin{cases} 0 & \text{if } (x_1,x_2) = (0,0),\\ \displaystyle{\frac{\text{max}(\lvert x_1 \rvert, \lvert x_2 \rvert )}{\sqrt{x_1^2 + x_2^2}}} ( x_1,x_2)& \text{otherwise.} \end{cases}
\end{equation}
This function maps for each \( 0 < d \leq 1 \), the border of each square \( \{ (x_1,x_2) \in \mathbb{R}^2 : \text{max}( \lvert x_1 \rvert, \lvert x_2 \rvert) \leq d \} \) into the circle of radius \( d \) centered at the origin; the manner in which these sets map into each other indicates why the function \( \varphi \) is a bijection. It is very easy to check its continuity as well, and I leave that task to the reader.
An inverse to this function is constructed in a similar way, so that each circle is mapped to the border of a square:
\begin{equation}
\varphi^{-1}(y_1,y_2) = \begin{cases} 0 & \text{if } (y_1,y_2) = (0,0),\\ \displaystyle{\frac{\sqrt{y_1^2+y_2^2}}{\text{max}(\lvert y_1\rvert, \lvert y_2\rvert)}}(y_1,y_2) & \text{otherwise.}\end{cases}
\end{equation}
An open interval and the real line
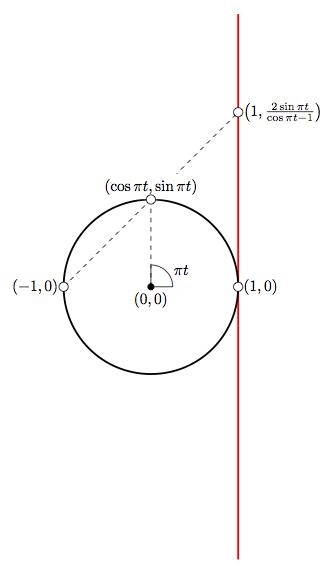
Let us find an homeomorphism from the unit interval \((-1,1)\) into the real line \(\mathbb{R}\) based in an interesting construction called stereographic projection. We start by mapping each \(t \in (-1,1)\) into an angle \(\theta \in (-\pi, \pi)\) by simple multiplication: \(\theta = \pi t\). This angle gives a single element in the unit circle \((\cos \pi t, \sin \pi t)\), except the point \((-1,0).\) The stereographic projection turns each point of the circle different than \((-1,0)\) into a unique point in the plane with coordinates \(\big(1,\varphi(t) \big),\) where
\begin{equation}
\varphi(t) = \displaystyle{ \frac{2\sin \pi t}{\cos \pi t +1} }.
\end{equation}
This is the function we are looking for. Its continuity is easy to prove, and so are its one-to-one and onto properties. In order to construct the inverse map, trace back from the real line to the vertical line \(\{(1,s) : s \in \mathbb{R}\},\) from there to the unit disk by the inverse of stereographic projection through the point \((-1,0)\), and find the angle of the corresponding image. Division by \(\pi\) offers you a value in the unit interval \((-1,1).\) This value is the image of the inverse \(\varphi^{-1}.\) I leave the construction of the analytical expression of this function to the reader as a nice exercise.