Let \( A=\mathbb{S}_1 \times \mathbb{S}_1 \), the product of two circles, and \( B \subset \mathbb{R}^3 \) the surface of revolution formed by rotation of the circle \( (x_1-2)^2+x_3^2=1 \) in the plane \( {x_2=0} \) around the \( z \)–axis:
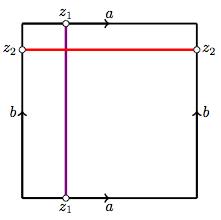
And last, consider in the unit square \( \square_2 = \{ (x_1,x_2) \in \mathbb{R}^2 : \lvert x_1 \rvert \leq 1, \lvert x_2 \rvert \leq 1\} \) the equivalence relation defined by \( (x_1,x_2) \sim (y_1,y_2) \) if one of the following is satisfied:
- \( x_1=y_1 \) and \( x_2=y_2 \), or
- \( \lvert x_1 \rvert = \lvert y_1 \rvert = 1 \) and \( x_2=y_2, \) or
- \( \lvert x_2 \rvert = \lvert y_2 \rvert = 1 \) and \( x_1=y_1. \)
Let \( C = \big( \square_2 / \sim \big), \) be the quotient set defined through equivalence classes from the relation above.
We want to prove that these three spaces \( A \), \( B \) and \( C \) are actually homeomorphic. In order to construct the corresponding homeomorphisms we will use the following intuitive ideas, as illustrated in the images of the sets below:
 |
|
 |
 |
For example, to find a homeomorphism \( \varphi_{AB} \colon A \to B, \) we consider a construction based on the following facts:
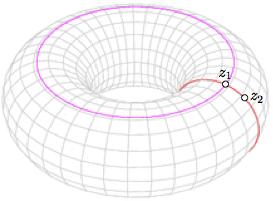
- The horizontal plane \( { z = 1 } \) intersects the torus \( B \) in a single circle (represented in pink). We identify the first copy of \( \mathbb{S}_1 \) in \( A=\mathbb{S}_1 \times \mathbb{S}_1 \) with this circle. Let us denote that pink circle \( B_1. \)
- Once chosen an element \( z_1 \) in the first copy of \( \mathbb{S}_1 \) from \( A \), we consider the corresponding point in \( B_1 \) from a suitable homeomorphism between \( \mathbb{S}_1 \) and \( B_1. \) Let us write \( z_1^\ast \in B_1. \)
- Consider the intersection of the torus \( B \) with a plane that goes through the origin, the point \( z_1^\ast \), and that is vertical. This intersections consists on two different circles, only one of which goes through the point \( z_1^\ast \) (represented in red); let us denote \( B_{z_1} \) this new circle, which we want to identify with the second copy of \( \mathbb{S}_1 \) in \( A. \)
- Once chosen an element \( z_2 \) in the second copy of \( \mathbb{S}_1 \) from \( A, \) consider the corresponding point in \( B_{z_1} \) from another suitable homeomorphism. We write \( z_2^\ast \in B_{z_1}. \)
I leave to the reader the pleasure of finding an analytic expression for this homeomorphism \( \varphi_{AB}. \)
To construct an homeomorphism \( \varphi_{CB} \colon C \to B \), we can proceed intuitively from a square piece of elastic material, and glue two parallel sides together as indicated in the diagram, thus forming a cylinder. It should not be too hard to construct a homeomorphism that turns a square into a cylinder in the Euclidean 3–dimensional space (use the correct coordinate system!) Notice that the bases of such cylinder (which correspond to the other parallel sides of the previous square) turned into circles. We can then glue both circles together as indicated in the diagram, thus forming a surface similar to that of \( B. \) This operation has also a nice analytic expression as a map from the cylinder to the torus, which once chosen the right coordinate system, should be no trouble to compute for the reader. The composition of these two homeomorphisms is, of course, an homeomorphism \( \varphi_{CB}. \)
Of course, to come up with the homeomorphism between \( A \) and \( C, \) we can make use of the two previous: \( \varphi_{AC} = \varphi_{CB}^{-1} \circ \varphi_{AB}, \) for example.