A triangulation of a compact surface \( S \) is a finite family of closed subsets \( { T_1, T_2, \dotsc, T_m} \) that cover \( S, \) and a family of homeomorphisms \( \varphi_k: \mathcal{T} \to T_k \), where \( \mathcal{T} \subset \mathbb{R}^2 \) is a proper triangle in the plane. We say that the sets \( T_k \) are triangles as well, and the images by \( \varphi_k \) of a vertex (resp. edge) of the triangle \( \mathcal{T} \) is also called a vertex (resp. edge). We impose one condition: Given two different triangles \( T_k \) and \( T_j, \) their intersection must be either void, or a common vertex, or a common edge.

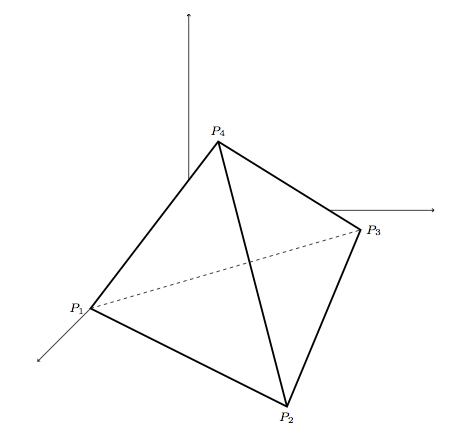
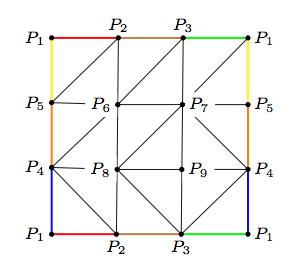
Since the (surface of a) tetrahedron is homeomorphic to the sphere \( \mathbb{S}_2, \) we may consider this as a valid triangulation for the latter. This triangulation is formed basically by four triangles, four vertices and six edges. The following example shows a triangulation of a torus, performed on the representation of \( \mathbb{T} \) given by the quotient space of the square \( \square_2 \) by the proper identification in the border. Note that in this representation, all of the vertices of the square are actually the same vertex, which we denote \( P_1. \) We construct a triangulation by placing two more vertices on the horizontal borders, \( P_2, P_3, \) two more vertices in the vertical borders, \( P_4, P_5, \), four more vertices inside the square, \( P_6, P_7, P_8, P_9, \), and joining all of them with edges, as shown in the image below: This gives the following triangles:

\begin{equation} \begin{array}{ccc}P_1P_2P_5 & P_2P_5P_6 & P_2P_3P_6\\P_3P_6P_7 & P_1P_3P_6 & P_1P_5P_7\\P_4P_5P_6 & P_4P_6P_8 & P_6P_7P_8\\P_7P_8P_9 & P_4P_7P_9 & P_4P_5P_7\\P_1P_2P_4 & P_2P_4P_8 & P_2P_3P_8\\P_3P_8P_9 & P_3P_4P_9 & P_1P_3P_4\end{array} \end{equation}

Two important observations about triangulations of any compact surface:

• Each edge belongs to exactly two triangles. This is due to the fact that the surfaces have at every point, a neighborhood that is homeomorphic to an open ball.
• Given a vertex \( v \) in a proper triangulation, it is possible to sort all the triangles that share than vertex, say clock or counterclockwise, in such a way that two consecutive triangles share a common edge. This is a direct consequence of the previous observation, and the fact that the union of all the triangles sharing a common vertex must be a connected set.